Question

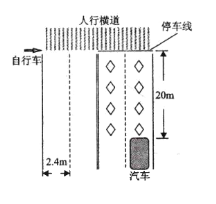
【题目】如图所示为某城市十字路口道路示意图，道路为双向四车道，每个车道宽度为2.4m。某自行车从道路左侧车道线沿停车线向右匀速行驶，速率为14. 4km/h，汽车在最右侧车道正中间行驶，速率为54km/h，汽车前端距离停车线20m。已知汽车的宽度与自行车的长度相等均为1. 8m，汽车的车身长4. 8m。汽车司机为避免与自行车相撞马上采取刹车制动，最大制动加速度大小为5m/s2.求

（1）汽车的最短刹车距离sm;

（2）请通过计算判断是否能够避免相撞。

Answer 1

【答案】（1）22. 5m .（2）不能避免相撞。

【解析】

(1)已知：

v1 =14.4km/h= 4m/s

v2 = 54km/h= 15m/s

设汽车以最大加速度刹车，则：

代入数据解得sm=22. 5m .

(2)以最大加速度刹车，设汽车车头到达停车线所用时间为t，则

解得t=2s或者t=4s，又因为汽车停下的时间为：

故t=4s不符题意，舍去；

此时以左侧车道线为起点，车头所占位置范围为s1~s2，

自行车在t=2s的时间内行驶的位移为x .则有：

自行车此时所占位置范围为：

由此可知，它们的位置范围有重叠，不能避免相撞.

答：（1）汽车的最短刹车距离sm=22. 5m;

（2）不能够避免相撞。