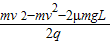题目内容
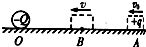
 如图所示,O、B、A为一粗糙绝缘水平面上的三点,一电荷量为-Q的点电荷固定在O点,现有一质量为m,电荷量为+q的小金属块(可视为质点),从A点以初速度v0沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v.已知小金属块与水平面间的动摩擦因数为μ,AB间距离为L、静电力常量为k,则( )
如图所示,O、B、A为一粗糙绝缘水平面上的三点,一电荷量为-Q的点电荷固定在O点,现有一质量为m,电荷量为+q的小金属块(可视为质点),从A点以初速度v0沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v.已知小金属块与水平面间的动摩擦因数为μ,AB间距离为L、静电力常量为k,则( )分析:金属块B点时速度最小,则知A到B过程,金属块做减速运动,B到O过程做加速运动,在B点金属块所受的滑动摩擦力与库仑力平衡.电场力做正功,电势能减小.根据库仑定律知,距离减小,库仑力增大,由牛顿第二定律分析加速度的变化情况.根据动能定理求解A、B两点的电势差.
解答:解:A、由题意知,A到B过程,金属块做减速运动,B到O过程做加速运动,在B点金属块所受的滑动摩擦力与库仑力平衡,则有 μmg=K
,得r=
.故A正确.
B、小金属块由A点向O点运动的过程中,电场力一直做正功,电势能一直减小.故B错误.
C、A到B过程,库仑力小于滑动摩擦力,库仑力增大,合力减小,加速度减小;B到O过程,库仑力大于滑动摩擦力,库仑力增大,合力增大,加速度增大;故C正确.
D、滑块从A到B过程,由动能定理得:qUAB-μmgL=
mv2-
m
,得UAB=
.故D错误.
故选AC
| r2 |
|
B、小金属块由A点向O点运动的过程中,电场力一直做正功,电势能一直减小.故B错误.
C、A到B过程,库仑力小于滑动摩擦力,库仑力增大,合力减小,加速度减小;B到O过程,库仑力大于滑动摩擦力,库仑力增大,合力增大,加速度增大;故C正确.
D、滑块从A到B过程,由动能定理得:qUAB-μmgL=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
2μmgL+mv2-m
| ||
| 2q |
故选AC
点评:本题的突破口是“B点速度最小”,分析金属块的运动情况,来分析其受力情况,由牛顿第二定律分析加速度的变化情况,根据动能定理求解电势差.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
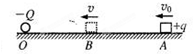 如图所示,O、B、A为一粗糙绝缘水平面上的三个点,三个点在同一条直线上,一电荷量为-Q的点电荷固定在O点,现有一质量为m,电荷量为+q的小金属块(可视为质点),从A点以初速度υ0沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为υ(υ<υ0).已知小金属块与水平面间的动摩擦因数为μ,AB间距离为L,静电引力常数为k,则( )
如图所示,O、B、A为一粗糙绝缘水平面上的三个点,三个点在同一条直线上,一电荷量为-Q的点电荷固定在O点,现有一质量为m,电荷量为+q的小金属块(可视为质点),从A点以初速度υ0沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为υ(υ<υ0).已知小金属块与水平面间的动摩擦因数为μ,AB间距离为L,静电引力常数为k,则( ) 沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v,已知小金属块与水平面间的动摩擦因数为μ,AB间距离为L,静电力常量为k,则
沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v,已知小金属块与水平面间的动摩擦因数为μ,AB间距离为L,静电力常量为k,则