题目内容
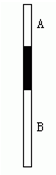 如图所示,两端封闭的直玻璃管用水银柱隔开两段空气柱A和B,已知VB>VA.若使两段空气柱同时升高相同的温度,水银柱将如何移动?对此,甲、乙两同学有不同的解法和结论:
如图所示,两端封闭的直玻璃管用水银柱隔开两段空气柱A和B,已知VB>VA.若使两段空气柱同时升高相同的温度,水银柱将如何移动?对此,甲、乙两同学有不同的解法和结论:甲同学:设两段空气柱压强不变,由盖?吕萨克定律,推出:△V=
| △T |
| T |
由VB>VA,得△VB>△VA,所以水银柱向上移动.乙同学:设两段空气柱体积不变,由查理定律,
推出:△P=
| △T |
| T |
请你作出评价:
(1)
(2)说明你的理由:
分析:该题使用假设法来解题.先假设水银柱不动,求出两部分气体的压强的增加量,若增加量相等,则水银柱不动;若增加量不相等,则水银柱向压强的增加量小的一边移动.
解答:评价:
(1)两段空气柱的体积的总和是保持不变的,所以同时升高相同的温度后,两段空气柱的压强一定会发生变化,故甲的假设出发点就存在着误区;具体来说,水银柱的移动是由于两段空气的压强变化不相等,从而引起对水银柱压力的变化不相等而引起的,所以不能假设气体的压强不变,甲的假设不成立.
乙同学设两段空气柱体积不变,从而导出两部分气体的压强的变化,两段空气的压强变化不相等,从而引起对水银柱压力的变化不相等,这时,水银柱将向压强变化较小的一方移动.故乙的回答是正确的.
(2)水银柱的移动是由于两段空气的压强变化不相等,从而引起对水银柱压力的变化不相等而引起的,所以不能假设气体的压强不变,甲的假设不成立,乙正确.(或:不能假设两段空气柱的压强不变,因为两段空气柱的总长度不变,所以不可能出现压强不变而气体长度同时变长、变短的情况,甲不正确.)
故答案为:乙;水银柱的移动是由于两段空气的压强变化不相等,从而引起对水银柱压力的变化不相等而引起的,所以不能假设气体的压强不变,甲的假设不成立,乙正确
(1)两段空气柱的体积的总和是保持不变的,所以同时升高相同的温度后,两段空气柱的压强一定会发生变化,故甲的假设出发点就存在着误区;具体来说,水银柱的移动是由于两段空气的压强变化不相等,从而引起对水银柱压力的变化不相等而引起的,所以不能假设气体的压强不变,甲的假设不成立.
乙同学设两段空气柱体积不变,从而导出两部分气体的压强的变化,两段空气的压强变化不相等,从而引起对水银柱压力的变化不相等,这时,水银柱将向压强变化较小的一方移动.故乙的回答是正确的.
(2)水银柱的移动是由于两段空气的压强变化不相等,从而引起对水银柱压力的变化不相等而引起的,所以不能假设气体的压强不变,甲的假设不成立,乙正确.(或:不能假设两段空气柱的压强不变,因为两段空气柱的总长度不变,所以不可能出现压强不变而气体长度同时变长、变短的情况,甲不正确.)
故答案为:乙;水银柱的移动是由于两段空气的压强变化不相等,从而引起对水银柱压力的变化不相等而引起的,所以不能假设气体的压强不变,甲的假设不成立,乙正确
点评:该类题目使用假设法来解题是关键.否则,则找不到突破的思路.属于基础题型,简单题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图所示,两端封闭的U形管位于竖直平面内,A、B管中一定质量的理想气体处于室温状态,开始时A、B管中的水银面相平,现使U形管在竖直平面内顺时针转过一个不大的角度,待管中水银柱稳定后,保持管转动后的姿态不变,则( )
如图所示,两端封闭的U形管位于竖直平面内,A、B管中一定质量的理想气体处于室温状态,开始时A、B管中的水银面相平,现使U形管在竖直平面内顺时针转过一个不大的角度,待管中水银柱稳定后,保持管转动后的姿态不变,则( ) 如图所示,两端封闭的均匀玻璃管竖直放置,管中间有一段水银柱将管中气体分成体积相等的两部分,管内气体的温度始终与环境温度相同.一段时间后,发现下面气体的体积比原来大了,则可以判断环境温度
如图所示,两端封闭的均匀玻璃管竖直放置,管中间有一段水银柱将管中气体分成体积相等的两部分,管内气体的温度始终与环境温度相同.一段时间后,发现下面气体的体积比原来大了,则可以判断环境温度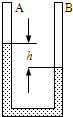 如图所示为两端封闭的U形玻璃管,竖直放置,管内左、右两段封闭空气柱A、B被一段水银柱隔开,设原来温度分别为TA和TB,当温度分别升高△TA和△TB时,关于水银柱高度差的变化情况,下列说法中正确的是( )
如图所示为两端封闭的U形玻璃管,竖直放置,管内左、右两段封闭空气柱A、B被一段水银柱隔开,设原来温度分别为TA和TB,当温度分别升高△TA和△TB时,关于水银柱高度差的变化情况,下列说法中正确的是( )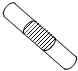 如图所示,两端封闭的玻璃管中间有一段水银柱,经适当倾斜,使上下两部分气体的体积恰好相等.保持管的倾角不变,管内气体的温度始终与环境温度相同,则( )
如图所示,两端封闭的玻璃管中间有一段水银柱,经适当倾斜,使上下两部分气体的体积恰好相等.保持管的倾角不变,管内气体的温度始终与环境温度相同,则( )