题目内容
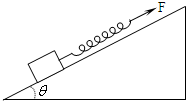 质量不计的弹簧下端固定一木块,平行地放在一斜面上,现手持弹簧上端使木块以相同大小的加速度a(a<gsinθ)分别沿斜面向上、向下匀加速运动.若斜面光滑,弹簧的伸长量分别为x1和x2;若物体与斜面间的动摩因数为μ,弹簧的伸长量分别为x1′和x2′,则
质量不计的弹簧下端固定一木块,平行地放在一斜面上,现手持弹簧上端使木块以相同大小的加速度a(a<gsinθ)分别沿斜面向上、向下匀加速运动.若斜面光滑,弹簧的伸长量分别为x1和x2;若物体与斜面间的动摩因数为μ,弹簧的伸长量分别为x1′和x2′,则
- A.x1+x2=x1′+x2′
- B.x1+x2>x1′+x2′
- C.x1+x2<x1′+x2′
- D.x1+x2′=x1′+x2
A
分析:分别列出向上和向下运动的牛顿第二定律表达式,由此可以得到形变量的关系.重点是:向下运动时由于加速度a(a<gsinθ),故而弹力向上.
解答:
向上运动时:
kx1-mgsinθ=ma①
向下运动时:
mgsinθ-kx2=ma②
由摩擦时:
向上运动时:
kx1′-mgsinθ-μmgcosθ=ma③
向下运动时:
mgsinθ-kx2′-μmgcosθ=ma④
由①②解得:
x1+x2=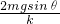
由③④解得:
x1′+x2′=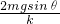
故:x1+x2=x1′+x2′,A正确.
故选A
点评:本题两个重点一是对摩擦力方向的判定,二是对弹力方向的判定,抓住这两点,应用牛顿第二定律就可以解答.
分析:分别列出向上和向下运动的牛顿第二定律表达式,由此可以得到形变量的关系.重点是:向下运动时由于加速度a(a<gsinθ),故而弹力向上.
解答:
向上运动时:
kx1-mgsinθ=ma①
向下运动时:
mgsinθ-kx2=ma②
由摩擦时:
向上运动时:
kx1′-mgsinθ-μmgcosθ=ma③
向下运动时:
mgsinθ-kx2′-μmgcosθ=ma④
由①②解得:
x1+x2=
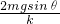
由③④解得:
x1′+x2′=
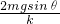
故:x1+x2=x1′+x2′,A正确.
故选A
点评:本题两个重点一是对摩擦力方向的判定,二是对弹力方向的判定,抓住这两点,应用牛顿第二定律就可以解答.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目