Question

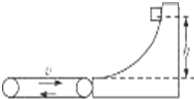
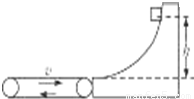
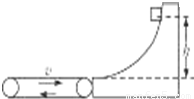
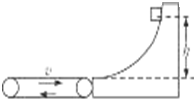一个水平方向足够长的传送带以恒定的速度3m/s沿顺时针方向转动，传送带右端固定着一个光滑曲面，并且与曲面相切，如图所示．小物块从曲面上高为h的P点由静止滑下，滑到传送带上继续向左运动，物块没有从左边滑离传送带．已知传送带与物体之间的动摩擦因数μ=0.2，不计物块滑过曲面与传送带交接处的能量损失，g取10m/s²．
（1）若h₁=1.25m，求物块返回曲面时上升的最大高度；
（2）若h₁=0.2m，求物块返回曲面时上升的最大高度．

Answer 1

分析：（1）根据动能定理求出物块下滑到曲面底端时速度大小，当物块的速度大于传送带的速度大小时，物块先减速到速度为零后，又返回做加速运动，当两者的速度相同时，以共同的速度一起匀速，直到滑上曲面．再根据动能定理求出物块返回曲面时上升的最大高度；
（2）用同样的方法研究．当物块滑上传送带的速度小于传送带的速度大小时，物块先减速到速度为零后，又返回做加速运动，到达曲面底端时速度与下滑时速度大小相等．

解答：解：（1）设物块滑到光滑曲面下端的速度为v₁，由动能定理得
   mgh₁=

1

2

m

v

2 1

解得：v₁=5m/s＞3m/s                               
所以物块先减速到速度为零后，又返回做加速运动，
当两者的速度相同时，以共同的速度v=3m/s一起匀速，直到滑上曲面．
设物块上升的高度H₁，由动能定理得，
 

1

2

mv2=mgH1
代入解得H₁=0.45m．
（2）若h₂=0.2m，根据动能定理得，
  mgh₂=

1

2

m

v

2 2

代入解得v₂=2m/s＜3m/s，所以物块先减速到速度为零后，又返回做加速运动，返回曲面底端时速度大小仍为2m/s，直到滑上曲面，上升的高度仍为0.2m．
答：
（1）若h₁=1.25m，物块返回曲面时上升的最大高度为0.45m；
（2）若h₁=0.2m，物块返回曲面时上升的最大高度为0.2m．

点评：本题关键是分析物块滑上传送带的运动过程，利用运动的对称性进行判断．中等难度．