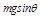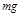题目内容
(12分)如图所示,质量为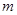 的小球用长为l 的轻质细线悬挂于O点,与O点处于同一水平线的P点处有一根光滑的细钉OP= l /2,已知,在A点给小球一个水平向左的初速度v0,发现小球恰好能到达跟P点在同一竖直线上的最高点B,则
的小球用长为l 的轻质细线悬挂于O点,与O点处于同一水平线的P点处有一根光滑的细钉OP= l /2,已知,在A点给小球一个水平向左的初速度v0,发现小球恰好能到达跟P点在同一竖直线上的最高点B,则
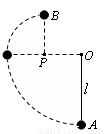
⑴小球到达B点时的速度是多大?
⑵若不计空气阻力,则给小球的初速度v0应该多大?
⑶若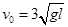 ,那么小球从点
,那么小球从点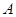 到
到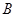 的过程中克服空气阻力做功为多少?
的过程中克服空气阻力做功为多少?
【答案】
(1) (2)
(2) (3)
(3)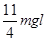
【解析】
试题分析:
(1)最高点B临界情况是绳子的拉力等于零,重力提供圆周运动所需的向心力,根据牛顿第二定律求出小球到达B点的速度.
(2)取A到B过程为研究过程,运用动能定理求出初速度.
(3)取A到B过程为研究过程,运用动能定理求出该过程中克服空气阻力所做的功.
解:(1)根据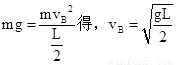 ,故小球到达B点的速度为
,故小球到达B点的速度为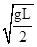 .
.
(2)不计空气阻力,在A到B的过程中,只有重力做功,根据动能定理得
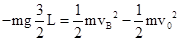 解得,
解得,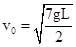 ,故不计空气阻力,则初速度v0为
,故不计空气阻力,则初速度v0为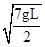 .
.
(3)根据动能定理得: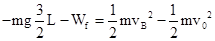
解得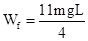 .
.
故小球从A到B的过程中克服空气阻力做功为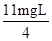 .
.
考点:动能定理的应用;机械能守恒定律.
点评:运用动能定理解题关键确定好研究的过程,判断在该过程中有哪些力做功,然后列表达式求解.

练习册系列答案
相关题目
 的小木块A 一水平初速度
的小木块A 一水平初速度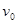 冲上质量M、长为
冲上质量M、长为 、置于光滑水平面的木块B ,并正好不从B木块上掉下,A、B间动摩擦因数为
、置于光滑水平面的木块B ,并正好不从B木块上掉下,A、B间动摩擦因数为 ,求此过程A、B物体组成的系统减少的动能。
,求此过程A、B物体组成的系统减少的动能。
 的小明静止悬挂时两橡皮绳的拉力大小均恰为
的小明静止悬挂时两橡皮绳的拉力大小均恰为 ,若此时小明左侧橡皮绳在腰间断裂,则小明此时
,若此时小明左侧橡皮绳在腰间断裂,则小明此时
 ,方向竖直向下
,方向竖直向下 ,方向沿未断裂绳的方向斜向上
,方向沿未断裂绳的方向斜向上 的小木块A 一水平初速度
的小木块A 一水平初速度 冲上质量M、长为
冲上质量M、长为 、置于光滑水平面的木块B ,并正好不从B木块上掉下,A、B间动摩擦因数为
、置于光滑水平面的木块B ,并正好不从B木块上掉下,A、B间动摩擦因数为 ,求此过程A、B物体组成的系统减少的动能。
,求此过程A、B物体组成的系统减少的动能。
 的小物体(可视为质点)静止地放在半径为
的小物体(可视为质点)静止地放在半径为 的半球体上,小物体与半球体间的动摩擦因数为
的半球体上,小物体与半球体间的动摩擦因数为 ,物体与球心的连线与水平地面的夹角为
,物体与球心的连线与水平地面的夹角为 ,整个装置静止。则下列说法正确的是 (
) 学
,整个装置静止。则下列说法正确的是 (
) 学 科网
科网