题目内容
20.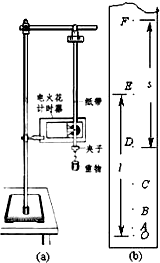 使用如图(a)所示的装置验证机械能守恒定律,打出一条纸带如图(b)所示.图(b)中O是打出的第一个点迹,A、B、C、D、E、F…是依次打出的点迹,量出OE间的距离为L,DF间的距离为S,已知打点计时器打点的周期是T.
使用如图(a)所示的装置验证机械能守恒定律,打出一条纸带如图(b)所示.图(b)中O是打出的第一个点迹,A、B、C、D、E、F…是依次打出的点迹,量出OE间的距离为L,DF间的距离为S,已知打点计时器打点的周期是T.①上述物理量如果在实验误差允许的范围内满足关系式8gl=$\frac{{s}^{2}}{{T}^{2}}$.即验证了重锤下落过程中机械能守恒.
②如果实验装置正确,仪器无损坏,周期T没变(T=0.02s),发现图(b)中OA距离大约是4mm,则出现这种情况的原因可能是先释放纸带,后启动打点计时器.
分析 (1)通过某段时间内平均速度等于中间时刻的瞬时速度求出E点的速度,从而得出动能的增加量,通过下落的高度求出重力势能的减小量,若动能的增加量和重力势能的减小量相等,则重锤下落过程中机械能守恒.
(2)若初速度为零,加速度为g,根据h=$\frac{1}{2}$gt2可知OA间的距离大约为2mm,若OA间实际的距离大于2mm,说明初速度不为零.
解答 解:(1)根据匀变速直线运动的规律可知,E点的速度为:
vE=$\frac{s}{2T}$
则O到E,动能的增加量为:△Ek=$\frac{1}{2}$m${v}_{E}^{2}$=$\frac{m{s}^{2}}{8{T}^{2}}$
重力势能的减小量△Ep=mgl,若△Ep=△Ek,即:8gl=$\frac{{s}^{2}}{{T}^{2}}$
(2)若初速度为零,加速度为g,则OA间的距离大约为:
h=$\frac{1}{2}$gt2≈2mm,若发现OA距离大约4mm,知初速度不为零,可能是先释放纸带后启动打点计时器.
故答案为:(1)8gl=$\frac{{s}^{2}}{{T}^{2}}$,(2)先释放纸带,后启动打点计时器.
点评 解决本题的关键掌握实验的原理,熟练应用匀变速直线运动的规律解答实验问题.

练习册系列答案
相关题目
10.质量相同的0℃冰和0℃水,下列说法正确的是( )
| A. | 它们的分子数不同,而分子的平均动能相同 | |
| B. | 它们的分子数相同,分子的平均动能也相同 | |
| C. | 分子的平均动能不同,冰小,水大 | |
| D. | 它们的内能不同,冰少,水多 |
11.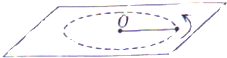 如图所示,小球m被一根细线拉着在光滑水平面上做匀速圆周运动,则关小、球m的受力分析,下列说法错误的是( )
如图所示,小球m被一根细线拉着在光滑水平面上做匀速圆周运动,则关小、球m的受力分析,下列说法错误的是( )
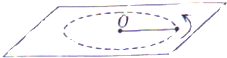 如图所示,小球m被一根细线拉着在光滑水平面上做匀速圆周运动,则关小、球m的受力分析,下列说法错误的是( )
如图所示,小球m被一根细线拉着在光滑水平面上做匀速圆周运动,则关小、球m的受力分析,下列说法错误的是( )| A. | 小球m受重力、支持力、绳的拉力和向心力的作用 | |
| B. | 小球m所受拉力的方向始终指向圆心 | |
| C. | 小球m所受重力和支持力是一对平衡力 | |
| D. | 小球m所受拉力提供它做匀速圆周运动所需的向心力 |
8.某行星的半径是地球半径的一半,1kg的物体在该行星表面所受的引力为19.6N,则该行星的质量是地球的( )
| A. | 2倍 | B. | 1倍 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
15.对于平抛运动,下列条件中可确定物体飞行时间的是( )
| A. | 下落高度 | B. | 水平位移 | C. | 初速度的大小 | D. | 末速度的大小 |
5.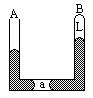 A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )
A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )
 A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )
A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )| A. | A端水银上升,B端水银下降 | |
| B. | A、B两端水银面都上升,但水银面高度差变小 | |
| C. | A、B两端水银面都上升,但水银面高度差变大 | |
| D. | A、B两端水银面都上升,但水银面高度差不变 |
12. 如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q电荷为圆心,半径为$\frac{L}{2}$画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线垂直于MN,一电荷量为+q的试探电荷在圆周上运动,则下列判断正确的是( )
如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q电荷为圆心,半径为$\frac{L}{2}$画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线垂直于MN,一电荷量为+q的试探电荷在圆周上运动,则下列判断正确的是( )
 如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q电荷为圆心,半径为$\frac{L}{2}$画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线垂直于MN,一电荷量为+q的试探电荷在圆周上运动,则下列判断正确的是( )
如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q电荷为圆心,半径为$\frac{L}{2}$画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线垂直于MN,一电荷量为+q的试探电荷在圆周上运动,则下列判断正确的是( )| A. | 电荷+q在a处所受到的电场力最大 | B. | a处的电势最高 | ||
| C. | b、c处的电场强度相同 | D. | 电荷+q从c运动到d,电场力做正功 |
9.下列说法正确的是( )
| A. | 只有物体温度较高时,才能向外辐射红外线 | |
| B. | 紫外线的主要作用是化学作用和荧光作用 | |
| C. | 可见光比红外线容易发生衍射现象 | |
| D. | X射线能在磁场中偏转,穿透力较强,可用来进行人体透视 |
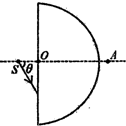 如图所示,一个半径为R、折射率为$\sqrt{3}$的透明玻璃半球体,O为球心,轴线OA水平且与半球体的左边界垂直.位于轴线上0点左侧$\frac{R}{3}$处的点光源S发出一束与OA夹角θ=60°的光线射向半球体.已知光在真空中传播的速度为c.
如图所示,一个半径为R、折射率为$\sqrt{3}$的透明玻璃半球体,O为球心,轴线OA水平且与半球体的左边界垂直.位于轴线上0点左侧$\frac{R}{3}$处的点光源S发出一束与OA夹角θ=60°的光线射向半球体.已知光在真空中传播的速度为c.