题目内容
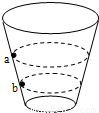
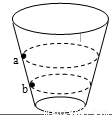
如图所示,为表演杂技“飞车走壁“的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的侧向摩擦,下列说法中正确的是( )
| A.在a轨道上运动时角速度较大 |
| B.在a轨道上运动时线速度较大 |
| C.在a轨道上运动时摩托车对侧壁的压力较大 |
| D.在a、b轨道上运动时摩托车和运动员所受的向心力相等 |

A、以任摩托车为研究对象,作出力图,如图.设侧壁与竖直方向的夹角为θ,
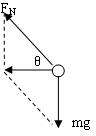
则根据牛顿第二定律,
得mgcotθ=mω2r,得到ω=
,θ相同,r大,则ω大,故在a轨道上运动时角速度较小.故A错误.
B、mgcotθ=m
解得v=
r大,则v大,则在a轨道上运动时线速度较大.故B正确.
C、设侧壁对车的支持力为FN,则由图得到
FN=
,因两车质量大小不知道,故无法比较FN的大小.故C错误.
D、向心力Fn=mgtanθ,因两车质量大小不知道,故无法比较Fn的大小.故D错误
故选B

则根据牛顿第二定律,
得mgcotθ=mω2r,得到ω=
|
B、mgcotθ=m
| v2 |
| r |
解得v=
| grcotθ |
r大,则v大,则在a轨道上运动时线速度较大.故B正确.
C、设侧壁对车的支持力为FN,则由图得到
FN=
| mg |
| sinθ |
D、向心力Fn=mgtanθ,因两车质量大小不知道,故无法比较Fn的大小.故D错误
故选B

练习册系列答案
相关题目
 如图所示,为表演杂技“飞车走壁“的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的侧向摩擦,下列说法中正确的是( )
如图所示,为表演杂技“飞车走壁“的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的侧向摩擦,下列说法中正确的是( )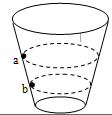 如图所示,为表演杂技“飞车走壁“的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的侧向摩擦,下列说法中正确的是( )
如图所示,为表演杂技“飞车走壁“的示意图.演员骑摩托车在一个圆桶形结构的内壁上飞驰,做匀速圆周运动.图中a、b两个虚线圆表示同一位演员骑同一辆摩托,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的侧向摩擦,下列说法中正确的是( )