题目内容
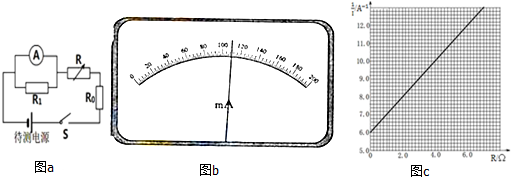
18.利用如图(a)所示电路,可以测量电源的电动势和内阻,所用的实验器材有:待测电源,电阻箱R(最大阻值999.9Ω),电阻R0(阻值为3.0Ω),电阻R1(阻值为3.0Ω),电流表A(量程为200mA,内阻为RA=6.0Ω),开关S.实验步骤如下:①将电阻箱阻值调到最大,闭合开关S;
②多次调节电阻箱,记下电流表的示数I和电阻箱相应的阻值R2;
③以$\frac{1}{I}$为纵坐标,R为横坐标,作$\frac{1}{I}$-R图线(用直线拟合);
④求出直线的斜率k和纵轴上的截距b.
回答下列问题:
(1)实验得到的部分数据如下表所示,其中电阻R=3.0Ω时电流表的示数如图(b)所示,读出数据,完成下表.答:①0.110,②9.09.
(2)根据图(c)图线求得斜率k=1.0A-1Ω-1,截距b=0.6A-1.
(3)分别用E和r表示电源的电动势和内阻,则$\frac{1}{I}$与R的关系式为$\frac{1}{I}$=$\frac{3}{E}$R+$\frac{3}{E}$(5.0+r)
| R/Ω | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
| I/A | 0.143 | 0.125 | ① | 0.100 | 0.091 | 0.084 | 0.077 |
| I-1/A-1 | 6.99 | 8.00 | ② | 10.0 | 11.0 | 11.9 | 13.0 |
分析 (1)根据图b所示电流表读出其示数,然后答题.
(2)应用描点法作出图象,然后根据图象分析答题.
(3)根据图a所示电路图应用欧姆定律求出图象的函数表达式.
(4)根据图象与图象的函数表达式求出电源电动势与内阻.
解答 解:(1)由图b所示可知,电流I=0.110A,故电流的倒数为9.09;
(2)根据表中实验数据在坐标系内描出对应点,然后作出图象如图所示: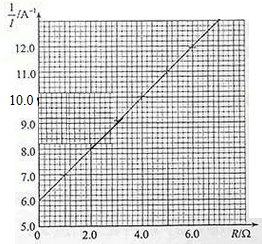
由图示图象可知,图象斜率k=$\frac{△\frac{1}{I}}{△R}$=$\frac{12-6}{6}$=1,由图示可知,图象截距:b=6.0;
(3)电流表与电阻R1并联,两端电压相等,电阻R1的阻值为3.0Ω,电流表内阻为RA=6.0Ω,则通过电阻R1的电流为为通过电流表的2倍,
电流表示数为I,电路电流为3I,并联电阻R并=2Ω,由图a所示电路图可知,E=3I(R并+R0+R+r),则$\frac{1}{I}$=$\frac{3}{E}$R+3$\frac{{R}_{并}+{R}_{0}+r}{E}$=$\frac{3}{E}$R+$\frac{3}{E}$(5.0+r);
(4)由图示图象与图象的函数表达式可知,k=$\frac{3}{E}$,b=$\frac{3}{E}$(5.0+r),代入数据解得,电源电动势E=3.0V时,内阻r=1.0Ω;
故答案为:(1)①0.110;②9.09;
(2)1;6.0;
(3)$\frac{1}{I}$=$\frac{3}{E}$R+$\frac{3}{E}$(5.0+r);
(4)3.0;1.0;
点评 本题考查了求图象函数表达式、电表读数、作图象、求电源电动势与内阻问题,应用图象法处理实验数据是常用的实验数据处理方法,要掌握描点法作图的方法,要会用图象法处理实验数据.

A、把打点计时器固定在桌子上 B、安好纸带
C、松开纸带让物体带着纸带运动 D、接通低压交流电源
E、取下纸带 F、断开开关
这些步骤正确的排列顺序为ABDCFE.
(2)用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图所示,每两个相邻的计数点之间还有4个打印点未画出.

①试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入下表要求保留3位有效数字.
| VB | VC | VD | VE | FF | |
| 数值(m/s) | 0.479 | 0.560 | 0.640 |
| A. | 玻尔理论成功地解释了各种原子的发光现象 | |
| B. | 爱因斯坦成功地解释了光电效应现象 | |
| C. | 汤姆生发现电子,表明原子具有核式结构 | |
| D. | 卢瑟福首先发现了铀和含铀的矿物质具有天然放射现象 |
| A. | 利用光谱分析鉴别物质只能是明线光谱或暗线光谱 | |
| B. | 汤姆孙发现了电子,表明原子具有核式结构 | |
| C. | 卢瑟福的α粒子散射实验,揭示了原子核具有复杂的结构 | |
| D. | 玻尔对原子模型提出了三点假设,成功解释了各种原子发光现象 |
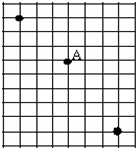 (1)在做“研究平抛物体的运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是BE
(1)在做“研究平抛物体的运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是BE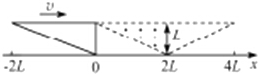 如图所示,等腰三角形的左半部分区域内分布有垂直于纸面向外的匀强磁场,其顶点在x轴上且底边长为4L,高为L,底边与x轴平行,纸面内一直角边长为L和2L的直角三角形导线框以恒定速度沿x轴正方形穿过磁场区域.t=0时刻导线框恰好位于图中所示的位置.规定顺时针方向为导线框中电流的正方向,下列能够正确表示电流一位移(i-x)关系的是( )
如图所示,等腰三角形的左半部分区域内分布有垂直于纸面向外的匀强磁场,其顶点在x轴上且底边长为4L,高为L,底边与x轴平行,纸面内一直角边长为L和2L的直角三角形导线框以恒定速度沿x轴正方形穿过磁场区域.t=0时刻导线框恰好位于图中所示的位置.规定顺时针方向为导线框中电流的正方向,下列能够正确表示电流一位移(i-x)关系的是( )



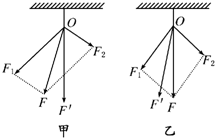 在“探究求合力的方法”时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳,实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.试回答下列问题:
在“探究求合力的方法”时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳,实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.试回答下列问题: