题目内容
12.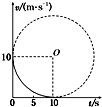 质点沿直线运动,在10s内其速度由10m/s减为0,速度随时间变化的关系图象即v-t图象,恰好是与两坐标轴相切的四分之一圆弧,如图所示,该质点在第5s末时的加速度大小为( )
质点沿直线运动,在10s内其速度由10m/s减为0,速度随时间变化的关系图象即v-t图象,恰好是与两坐标轴相切的四分之一圆弧,如图所示,该质点在第5s末时的加速度大小为( )| A. | $\frac{\sqrt{2}}{2}$ m/s2 | B. | $\frac{\sqrt{2}}{3}$ m/s2 | C. | $\frac{\sqrt{3}}{2}$ m/s2 | D. | $\frac{\sqrt{3}}{3}$ m/s2 |
分析 由图读出速度的变化情况,分析物体的运动情况.速度图象的斜率等于加速度.由图线“面积”求出位移,根据运动学基本公式及几何关系求解.
解答 解:如图所示,过5s对应的圆弧上的B点作切线EF,设圆弧的半径为R,由图形易得:
sinθ=$\frac{BC}{O′B}$=$\frac{\frac{R}{2}}{R}$=0.5,解得:θ=30°
由图中几何关系可知,△EOF~△O′CB,故:
tanθ=$\frac{BC}{O′C}$=$\frac{OF}{OE}$
因速度图象的斜率表示加速度的大小,则:
加速度为:a=tan∠OEF=$\frac{OF}{OE}$=$\frac{BC}{O′C}$
由加速度的概念知:BC应表示的是速度,O′C表示的是时间.
在△O′BC中,BC=O′Bsinθ,因BC表示的是速度,故
O′B=O′D=AO=10(m/s)
BC=10?sin30°=5(m/s).
在△O′BC中,O′C=O′Bcosθ,因O′C表示的是时间,故O′B=O′A=DO=10(s)
O′C=10?cos30°=5$\sqrt{3}$(s)
所以加速度:a=$\frac{BC}{O′C}$=$\frac{5}{5\sqrt{3}}$=$\frac{\sqrt{3}}{3}$m/s2
故选:D.
点评 本题关键抓住速度图象的斜率表示加速度、“面积”表示位移来理解图象的物理意义,并能结合几何关系求解.

练习册系列答案
相关题目
3.在下列物理过程中,机械能守恒的有( )
| A. | 把一个物体竖直向上匀速提升的过程 | |
| B. | 从地面上发射人造卫星升空的过程 | |
| C. | 汽车关闭油门后沿水平公路向前滑行的过程 | |
| D. | 从高处竖直下落的物体落在竖直的弹簧上,压缩弹簧的过程,对弹簧,物体和地球这一系统 |
20.物体做匀加速直线运动,在时间T内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则物体( )
| A. | 在A点的速度大小为$\frac{{{x_2}-{x_1}}}{2T}$ | B. | 在B点的速度大小为$\frac{3{x}_{2}-{x}_{1}}{2T}$ | ||
| C. | 运动的加速度为$\frac{2{x}_{1}}{{T}^{2}}$ | D. | 运动的加速度为$\frac{{x}_{1}+{x}_{2}}{{T}^{2}}$ |
7.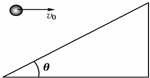 如图所示,倾角为θ的斜面正上方有一小球以初速度v0水平抛出.若小球到达斜面的位移最小,重力加速度为g,则飞行时间t为( )
如图所示,倾角为θ的斜面正上方有一小球以初速度v0水平抛出.若小球到达斜面的位移最小,重力加速度为g,则飞行时间t为( )
 如图所示,倾角为θ的斜面正上方有一小球以初速度v0水平抛出.若小球到达斜面的位移最小,重力加速度为g,则飞行时间t为( )
如图所示,倾角为θ的斜面正上方有一小球以初速度v0水平抛出.若小球到达斜面的位移最小,重力加速度为g,则飞行时间t为( )| A. | t=$\frac{2{v}_{0}cotθ}{g}$ | B. | t=v0tan θ | C. | t=$\frac{{v}_{0}cotθ}{g}$ | D. | t=$\frac{2{v}_{0}tanθ}{g}$ |
17.一个N匝圆线圈,放在磁感强度为B的匀强磁场中,线圈平面跟磁感强度方向成30°角,磁感强度随时间均匀变化,线圈导线粗细均匀,下列方法中可使线圈中感应电流增加一倍的是( )
| A. | 将线圈匝数增加一倍 | B. | 将线圈面积增加一倍 | ||
| C. | 将线圈半径增加一倍 | D. | 减小线圈平面与磁场的夹角 |
1.真空中两个电量为2Q和-Q点电荷,相距为L,则它们连线中点处的电场强度为( )
| A. | 0 | B. | k$\frac{4Q}{{L}^{2}}$ | C. | k$\frac{8Q}{{L}^{2}}$ | D. | k$\frac{12Q}{{L}^{2}}$ |
2. 如图所示,图线a是线圈在匀强磁场中匀速转动时产生的正弦交流电的图象,当只改变线圈的转速后,产生正弦交流电的图象如图线b所示,以下说法正确的是( )
如图所示,图线a是线圈在匀强磁场中匀速转动时产生的正弦交流电的图象,当只改变线圈的转速后,产生正弦交流电的图象如图线b所示,以下说法正确的是( )
 如图所示,图线a是线圈在匀强磁场中匀速转动时产生的正弦交流电的图象,当只改变线圈的转速后,产生正弦交流电的图象如图线b所示,以下说法正确的是( )
如图所示,图线a是线圈在匀强磁场中匀速转动时产生的正弦交流电的图象,当只改变线圈的转速后,产生正弦交流电的图象如图线b所示,以下说法正确的是( )| A. | 线圈先后两次转速之比为2:3 | |
| B. | 通过线圈的磁通量最大值之比为3:2 | |
| C. | 先后两次交流电的最大值之比为3:2 | |
| D. | 先后两次交流电的有效值之比为3:2 |

 如图所示,一面积为S的线圈内有理想边界的磁场,当磁场均匀增加时,有一带电粒子静止于平行板(两板水平放置)电容器中间,若线圈的匝数为n,平行板电容器的板间距离为d,粒子的质量为m,带电量为q,则:此粒子带什么电,磁感应强度的变化率是多少.
如图所示,一面积为S的线圈内有理想边界的磁场,当磁场均匀增加时,有一带电粒子静止于平行板(两板水平放置)电容器中间,若线圈的匝数为n,平行板电容器的板间距离为d,粒子的质量为m,带电量为q,则:此粒子带什么电,磁感应强度的变化率是多少.