题目内容
 如图,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量分别为m和2m的两小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆由水平位置静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力.下列说法正确的是( )
如图,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量分别为m和2m的两小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆由水平位置静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力.下列说法正确的是( )A.在竖直位置两球的速度大小均为

B.杆竖直位置时对m球的作用力向上,大小为
 mg
mgC.杆竖直位置时铁钉对杆的作用力向上,大小为
 mg
mgD.由于忽略一切摩擦阻力,根据机械能守恒,杆一定能绕铁钉做完整的圆周运动
【答案】分析:将轻杆从水平位置由静止释放,转到竖直位置时,A、B两球的速度大小相等,根据系统的机械能守恒,求出速度大小.对B研究,根据牛顿第二定律求解杆的作用力大小和方向,分析机械能的变化,判断A的机械能是否守恒.
解答:解:A、将轻杆从水平位置由静止释放,转到竖直位置时,两球的速度大小相等,设为v,根据系统的机械能守恒,得
2mgL-mgL= ?3mv2,解得,v=
?3mv2,解得,v=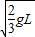 .故A错误.
.故A错误.
B、杆转到竖直位置时,对m球:mg-N=m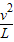 ,解得,N=
,解得,N=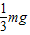 ,故B错误;
,故B错误;
C、杆转到竖直位置时,对2m球:N′-2mg=2m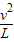 ,解得,N′=
,解得,N′=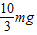 ,所以铁钉对杆的作用力向上,大小为N+N′=
,所以铁钉对杆的作用力向上,大小为N+N′=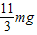 ,故C正确;
,故C正确;
D、由机械能守恒定律分析得知,当系统顺时针转到水平位置时速度为零,然后再逆时针转动,不可能做完整的圆周运动.故D错误.
故选C
点评:本题是轻杆连接的模型问题,对系统机械能是守恒的,但对单个小球机械能并不守恒,运用系统机械能守恒和牛顿运动定律结合研究.
解答:解:A、将轻杆从水平位置由静止释放,转到竖直位置时,两球的速度大小相等,设为v,根据系统的机械能守恒,得
2mgL-mgL=
 ?3mv2,解得,v=
?3mv2,解得,v=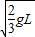 .故A错误.
.故A错误.B、杆转到竖直位置时,对m球:mg-N=m
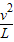 ,解得,N=
,解得,N=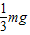 ,故B错误;
,故B错误;C、杆转到竖直位置时,对2m球:N′-2mg=2m
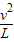 ,解得,N′=
,解得,N′=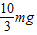 ,所以铁钉对杆的作用力向上,大小为N+N′=
,所以铁钉对杆的作用力向上,大小为N+N′=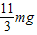 ,故C正确;
,故C正确;D、由机械能守恒定律分析得知,当系统顺时针转到水平位置时速度为零,然后再逆时针转动,不可能做完整的圆周运动.故D错误.
故选C
点评:本题是轻杆连接的模型问题,对系统机械能是守恒的,但对单个小球机械能并不守恒,运用系统机械能守恒和牛顿运动定律结合研究.

练习册系列答案
相关题目
 如图,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量分别为m和2m的两小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆由水平位置静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力.下列说法正确的是( )
如图,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量分别为m和2m的两小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆由水平位置静止释放,转到竖直位置,在转动的过程中,忽略空气的阻力.下列说法正确的是( ) 如图,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量分别为2m和3m的两小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆由水平位置静止释放,在转动的过程中,忽略空气的阻力及一切摩擦.下列说法正确的是( )
如图,一长为2L的轻杆中央有一光滑的小孔O,两端各固定质量分别为2m和3m的两小球,光滑的铁钉穿过小孔垂直钉在竖直的墙壁上,将轻杆由水平位置静止释放,在转动的过程中,忽略空气的阻力及一切摩擦.下列说法正确的是( ) A.两球的速度大小相等为
A.两球的速度大小相等为
