题目内容
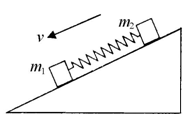
斜面上有m1和m2两个质量均为1㎏物体置于倾角为30°光滑斜面上，两物体间用一根轻质弹簧连接，m1通过一细绳固定于墙面，m2在沿斜面向上的力F=12N作用下沿斜面加速上滑，如图所示，当m2加速度达到1m/s2时突然撤去F，则下列说法正确的是（ ）分析：以m2为研究对象，根据牛顿第二定律求出m2加速度达到1m/s2时弹簧的弹力大小，突然撤去F时，弹簧的弹力大小没有变化，再根据牛顿第二定律求解两物体的加速度大小．
解答：解：设m2加速度达到1m/s2时弹簧的弹力大小为f，根据牛顿第二定律得
对m2：F-f-mgsinα=ma
解得，f=F-mgsinα-ma=12N-1×10×
N-1×1N=6N，
突然撤去F时，弹簧的弹力大小没有变化，则m2所受的合力大小为f+mgsinα，方向沿斜面向下，m1所受的合力没有变化，仍为零，根据牛顿第二定律得
对m2：f+mgsinα=ma2，代入解得a2=11m/s2
对m1：a1=0
即m1的加速度为零，m2的加速度立即变为11 m/s2．
故选C
对m2：F-f-mgsinα=ma
解得，f=F-mgsinα-ma=12N-1×10×
| 1 |
| 2 |
突然撤去F时，弹簧的弹力大小没有变化，则m2所受的合力大小为f+mgsinα，方向沿斜面向下，m1所受的合力没有变化，仍为零，根据牛顿第二定律得
对m2：f+mgsinα=ma2，代入解得a2=11m/s2
对m1：a1=0
即m1的加速度为零，m2的加速度立即变为11 m/s2．
故选C
点评：本题是瞬间问题，是牛顿第二定律运用中典型的问题，往往先研究状态变化前的情况，再研究状态变化后的情况．
练习册系列答案
科学实验活动册系列答案
相关题目
斜面上有m1和m2两个物体，与斜面间的动摩擦因数分别为μ1和μ2，两物体间用一根轻质弹簧连接，一起沿斜面减速上滑，如右图所示，在一起上滑的过程中，m1和m2之间的相对距离保持不变，弹簧的长度小于原长，则以下说法正确的是（ ）
如图所示，斜面上有m1和m2两个物体，与斜面间的动摩擦因数分别为μ1和μ2，两个物体间用一根轻质弹簧连接，恰好能一起沿斜面匀速下滑，则下列说法正确的是（ ）
