��Ŀ����
����Ŀ����ͼ���������Ϊd����б�̶�ƽ�н������죬λ����ˮƽ���ȷ��ͬһƽ���ڣ����Ҷ˽�һ��ֵΪR�ĵ��裬������費�ơ�����Ϊm������Ϊr�Ľ�����CD��ֹ�ڵ����ϣ����뵼���Ķ�Ħ������Ϊ����������ǿ�ų�����MNPQ����ֱ����ƽ�����£��őhӦǿ�ȴ�СΪB���ų��������ٶ�v0�ص�����������ɨ�������ˣ��ų��߽�PQ������˷���ʱ�˵��ٶ�Ϊ�����������㹻���������˶�������ʼ���뵼�촹ֱ���뵼�챣�����ýӴ�����
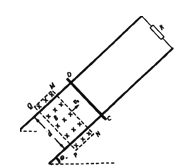
��1��MN�յ��������ʱ�����и�Ӧ�����Ĵ�С�ͷ���
��2��MN�յ��������ʱ���˵ļ��ٶȴ�С��
��3��PQ������˷���ʱ��R�ϵĵ繦�ʣ�
��4���������˵������MN�յ�������˵�PQ������˷������ι����У����������������˶���
���𰸡���1��![]() ����Ӧ���������Dָ��C����2��
����Ӧ���������Dָ��C����2��![]() ��gsin������gcos������3��
��gsin������gcos������3��![]() ����4��PQ������˷���ʱ�����
����4��PQ������˷���ʱ�����![]() ��������������ٶȼ�С�ļ����˶��������
��������������ٶȼ�С�ļ����˶��������![]() ��������������PQ����֮ʱ����������С�ոռ�С���뻬��Ħ������С��ȣ�������������ٶȼ�С�ļ����˶�������������PQ����֮ǰ����������С�Ѿ���С���뻬��Ħ������С��ȣ���������������ٶȼ�С�ļ����˶����������˶�
��������������PQ����֮ʱ����������С�ոռ�С���뻬��Ħ������С��ȣ�������������ٶȼ�С�ļ����˶�������������PQ����֮ǰ����������С�Ѿ���С���뻬��Ħ������С��ȣ���������������ٶȼ�С�ļ����˶����������˶�
��������
��1��MN�յ��������ʱ������E��Bdv0����˲����ĸ�Ӧ�綯�ƣ���ŷķ��������и�Ӧ�����Ĵ�С�������ֶ����жϸ�Ӧ�����ķ���
��2��MN�յ��������ʱ�������˵����������������ܵ��İ�����������˵ļ��ٶȴ�С��
��3��PQ������˷���ʱ�����ݷ����ڶ��ɡ�ŷķ���������·�е���������R�ϵĵ繦�ʣ�
��4����MN�յ�������˵�PQ������˷������ι����У����ݸ��ܵ��İ������������ص���ķ����ͻ���Ħ�����ĺ�����С��ϵ�����жϽ����˵��˶����
��1��MN�յ��������ʱ�����и�Ӧ�綯�� E��Bdv0
���и�Ӧ�����Ĵ�С ![]()
�����ֶ���֪���и�Ӧ���������Dָ��C��
��2��MN�յ��������ʱ���˵����������ͼ��ʾ��
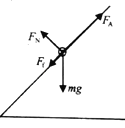
��б�淽����ţ�ٵڶ����ɵ�
FA��mgsin����Ff��ma
��ֱ��б�淽������ƽ�⣬�� N��mgcos����0
����Ħ���� Ff����N
������ FA��BId
������ã��˵ļ��ٶȴ�С a��![]() ��gsin������gcos��
��gsin������gcos��
��3��PQ������˷���ʱ�����и�Ӧ�綯�� E��Bd��v0��v��
���и�Ӧ�����Ĵ�С I��![]()
R�ϵĵ繦�� P��I2R��![]() ��
��
��4���ų�����ɨ�������˵Ĺ����У�����ţ�ٵڶ�������
![]() ����mgsin��+��mgcos������ma
����mgsin��+��mgcos������ma
���Ž����˵��ٶ������ٶȼ�С
PQ������˷���ʱ
�����![]() ����mgsin��+��mgcos������������������ٶȼ�С�ļ����˶���
����mgsin��+��mgcos������������������ٶȼ�С�ļ����˶���
�����![]() ����mgsin��+��mgcos������������������PQ����֮ʱ����������С�ոռ�С���뻬��Ħ������С��ȣ�������������ٶȼ�С�ļ����˶���
����mgsin��+��mgcos������������������PQ����֮ʱ����������С�ոռ�С���뻬��Ħ������С��ȣ�������������ٶȼ�С�ļ����˶���
����������PQ����֮ǰ����������С�Ѿ���С���뻬��Ħ������С��ȣ���������������ٶȼ�С�ļ����˶����������˶���

 ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�