题目内容
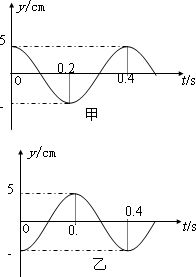
A和B是一列简谐横波在传播方向上的两质点,图中甲和乙分别为其振动图象,其平衡位置的坐标分是xA=0和xB=6m,如果波长大于3m但小于9m,波沿x轴正方向传播,求波的传播速度大小并画出t=0.1s时刻两质点间的波形图.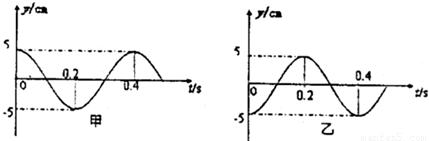
【答案】分析:由振动图象读出同一时刻A、B两个质点的状态,结合波形,得到两质点间的距离与波长的关系,求出波长,求出波速的通项,再结合条件求解波速的特殊值.根据A、B两个质点的状态画出波形.
解答:解:由振动图象看出,t=0时刻,A质点位于波峰,B质点位于波谷,则两质点间距离△x=(2n+1)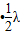 ,(n=0,1,2,…),
,(n=0,1,2,…),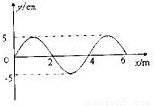
则得 λ=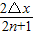 =
=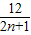 m
m
由题知,3m<λ<9m
则应取n=1,故λ=4m
由图知周期T=0.4s
所以波速v=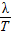 =10m/s
=10m/s
t=0.1时刻,A质点位于平衡位置向下,B位于平衡位置向上,则t=0.1s时刻两质点间的波形图如图所示.
答:波的传播速度大小为10m/s,画出t=0.1s时刻两质点间的波形图如图所示.
点评:本题中两个质点振动情况总是相反,两质点间的距离是半个波长的奇数倍,由通项求特殊值是基本的方法.
解答:解:由振动图象看出,t=0时刻,A质点位于波峰,B质点位于波谷,则两质点间距离△x=(2n+1)
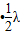 ,(n=0,1,2,…),
,(n=0,1,2,…),
则得 λ=
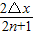 =
=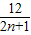 m
m由题知,3m<λ<9m
则应取n=1,故λ=4m
由图知周期T=0.4s
所以波速v=
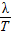 =10m/s
=10m/st=0.1时刻,A质点位于平衡位置向下,B位于平衡位置向上,则t=0.1s时刻两质点间的波形图如图所示.
答:波的传播速度大小为10m/s,画出t=0.1s时刻两质点间的波形图如图所示.
点评:本题中两个质点振动情况总是相反,两质点间的距离是半个波长的奇数倍,由通项求特殊值是基本的方法.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 (2007?广东)如图是一列简谐横波在某时刻的波形图,已知图中b位置的质点起振比a位置的质点晚0.5s,b和c之间的距离是5m,则此列波的波长和频率应分别为( )
(2007?广东)如图是一列简谐横波在某时刻的波形图,已知图中b位置的质点起振比a位置的质点晚0.5s,b和c之间的距离是5m,则此列波的波长和频率应分别为( )