题目内容
汽车A沿平直公路以速度v做匀速直线运动,当它路过某处的同时,有一汽车B开始做初速度为零、加速度为a的匀加速运动去追赶A车,根据上述条件,求:(1)B追上A所用的时间.
(2)B追上A时B的瞬时速度
(3)在追赶过程中,A和B之间何时有最大距离?这个距离是多少?
【答案】分析:(1)当两车位移相等时,B追上A,根据运动学公式求出时间.
(2)根据匀加速直线运动速度时间关系即可求解速度;
(3)在B追上A之前,A位于摩托车的前方.当B小于A的速度时,两者距离逐渐增大;当B大于A的速度时,两者距离逐渐减小;则两者速度相等时,两车之间的最远距离,由此条件求出时间,再求最大距离.
解答:解:(1)设经过时间t,摩托车能追上公共汽车,则有
 at2=vt
at2=vt
解得:t=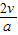
(2)根据v=at得:v=2v
(3)当两车速度相等时,两车之间的最远距离.
设经过时间t′两车速度相等,
t′=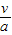
两者最大的距离S=vt′- at′2=
at′2=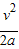
答:(1)B追上A所用的时间为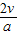 ;
;
(2)B追上A时B的瞬时速度为2v;
(3)在追赶过程中,经过时间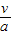 时A和B之间何时有最大距离,这个距离是
时A和B之间何时有最大距离,这个距离是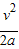
点评:本题也用图象法求解,根据图象很快得到两者速度相等时位移最大,难度适中.
(2)根据匀加速直线运动速度时间关系即可求解速度;
(3)在B追上A之前,A位于摩托车的前方.当B小于A的速度时,两者距离逐渐增大;当B大于A的速度时,两者距离逐渐减小;则两者速度相等时,两车之间的最远距离,由此条件求出时间,再求最大距离.
解答:解:(1)设经过时间t,摩托车能追上公共汽车,则有
 at2=vt
at2=vt解得:t=
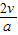
(2)根据v=at得:v=2v
(3)当两车速度相等时,两车之间的最远距离.
设经过时间t′两车速度相等,
t′=
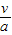
两者最大的距离S=vt′-
 at′2=
at′2=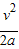
答:(1)B追上A所用的时间为
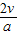 ;
;(2)B追上A时B的瞬时速度为2v;
(3)在追赶过程中,经过时间
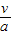 时A和B之间何时有最大距离,这个距离是
时A和B之间何时有最大距离,这个距离是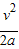
点评:本题也用图象法求解,根据图象很快得到两者速度相等时位移最大,难度适中.

练习册系列答案
相关题目