Question

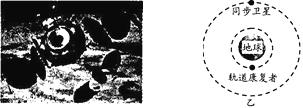
【题目】图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源，延长卫星的使用寿命。图乙是“轨道康复者”在某次拯救一颗地球同步卫星前，二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图，此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力，则下列说法正确的是

A. 在图示轨道上,“轨道康复者”的速度大于

B. 在图示轨道上,“轨道康复者”的加速度大小是地球同步卫星的4倍

C. 在图示轨道上,“轨道康复者”的周期为3h，且从图示位置开始经1.5h与同步卫星的距离最近

D. 若要对该同步卫星实施拯救,“轨道康复者”应从图示轨道上加速，然后与同步卫星对接

Answer 1

【答案】D

【解析】试题分析：A.由知第一宇宙速度是卫星的最大运行速度,“轨道康复者”的速度一定小于7.9km/s，故A错误；B.由牛顿第二定律可得，两者的轨道半径之比为1：4，所以加速度比为16：1，故B错误；C.两卫星从相距最远到相距最近需满足，，故C错误；D.“轨道康复者”从图示轨道上加速，则会做离心运动，从而接近同步轨道才能实现对接，故D正确。