Question

【题目】如图所示，bc为固定在小车上的水平横杆，物块M穿在杆上，靠摩擦力与杆保持相对静止，M又通过轻细线悬吊着一个小铁球m，此时小车以大小为a的加速度向右做匀加速运动，而M、m均相对小车静止，细线与竖直方向的夹角为小车的加速度逐渐增大，M始终和小车保持相对静止，当加速度增加到2a时　　

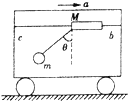
A. 细线与竖直方向的夹角增加到原来的2倍

B. 细线的拉力增加到原来的2倍

C. 横杆对M弹力增大

D. 横杆对M的摩擦力增加到原来的2倍

Answer 1

【答案】D

【解析】

以小球和物块整体为研究对象，分析受力，根据牛顿第二定律研究横杆对M的摩擦力、弹力与加速度的关系．对小球研究，根据牛顿第二定律，采用合成法研究细线与竖直方向的夹角、细线的拉力与加速度的关系。

A、B项：以小球为研究对象，分析受力情况如图所示

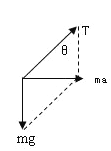
由牛顿第二定律得：mgtanθ=ma，得 ，当a增加到两倍时，tanθ变为两倍，但θ不是两倍。细线的拉力可见，a变为两倍，T不是两倍，故A、B错误；

C、D项：对小球和物块组成的整体，分析受力如图所示

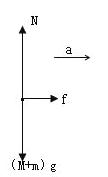
水平方向：f=（M+m）a，

竖直方向：N=（M+m）g。

则当加速度增加到2a时，横杆对M的摩擦力f增加到原来的2倍。横杆对M的弹力等于两个物体的总重力，保持不变，故C错误，D正确。

故应选：D。