题目内容
在A、B两题中选做一题A、已知大气压强是由于大气的重力而产生的.某学校兴趣小组想估算地球周围大气层空气的分子个数,通过查资料知道:地球半径R=6.4×106m,地球表面重力加速度g=10m/s2,大气压p0=1.0×105Pa,空气的平均摩尔质量M=2.9×10-2kg/mol,阿伏加德罗常数NA=6.0×1023mol-1.
(1)根据以上条件能估算出地球周围大气层空气的分子数吗?若能,请计算分子总数(保留一位有效数字);若不能,请说明理由.
(2)若月球半径r=1.7×106m,月球表面重力加速度g0=1.6m/s2,为开发月球的需要,设想在月球表面覆盖一层一定厚度的大气,若月球表面附近的大气压p0=1.0×105Pa,且已知大气层厚度比月球半径小得多,估算应给月球表面添加的大气层的总质量m.(保留一位有效数字)B、氢原于基态能量E1=-13.6eV,电子绕核做圆周运动的半径r1=0.53×10-10m.求
①氢原子处于n=5激发态时原子系统具有的能量;
①电子在n=3轨道上运动的动能(k=9.0×109N?m2/C2)(保留两位有效数字)
(1)根据以上条件能估算出地球周围大气层空气的分子数吗?若能,请计算分子总数(保留一位有效数字);若不能,请说明理由.
(2)若月球半径r=1.7×106m,月球表面重力加速度g0=1.6m/s2,为开发月球的需要,设想在月球表面覆盖一层一定厚度的大气,若月球表面附近的大气压p0=1.0×105Pa,且已知大气层厚度比月球半径小得多,估算应给月球表面添加的大气层的总质量m.(保留一位有效数字)B、氢原于基态能量E1=-13.6eV,电子绕核做圆周运动的半径r1=0.53×10-10m.求
①氢原子处于n=5激发态时原子系统具有的能量;
①电子在n=3轨道上运动的动能(k=9.0×109N?m2/C2)(保留两位有效数字)
分析:A、(1)根据大气压强是由于大气的重力而产生的,气体的重力等于气体对地球表面的压力,求出气体的质量,从而求出摩尔量,得出气体的分子数.
(2)根据气体重力等于气体对地球表面的压力求出月球表面添加的大气层的总质量m.
B、根据En=
求出处于激发态时原子系统具有的能量.
根据库仑引力提供向心力求出电子的速度,从而求出电子的动能.
(2)根据气体重力等于气体对地球表面的压力求出月球表面添加的大气层的总质量m.
B、根据En=
| E1 |
| n2 |
根据库仑引力提供向心力求出电子的速度,从而求出电子的动能.
解答:解:A、(1)能.因为4πp0R2=mg.
则气体的摩尔量n=
.
N=nNA.
则气体的分子数N=
.
代入数据可得N=1×1044.
(2)m0g0=4πp0r2.
m0=
,代入数据可得m0=2×1018kg.
答:(1)能,分子总数为1×1044.
(2)月球表面添加的大气层的总质量m0=2×1018kg.
①基态氢原子的能量E1=-13.6eV,
E5=
=-0.54eV.
②由k
=m
则Ek3=
.
r3=32r1
代入数据可得Ek3=1.5eV.
答:①氢原子处于n=5激发态时原子系统具有的能量为-0.54eV.
②电子在n=3轨道上运动的动能为1.5eV.
则气体的摩尔量n=
| m |
| M |
N=nNA.
则气体的分子数N=
| 4πNAp0R2 |
| Mg |
代入数据可得N=1×1044.
(2)m0g0=4πp0r2.
m0=
| 4πp0r2 |
| g0 |
答:(1)能,分子总数为1×1044.
(2)月球表面添加的大气层的总质量m0=2×1018kg.
①基态氢原子的能量E1=-13.6eV,
E5=
| E1 |
| 52 |
②由k
| e2 |
| r32 |
| v32 |
| r3 |
则Ek3=
| ke2 |
| 2r3 |
r3=32r1
代入数据可得Ek3=1.5eV.
答:①氢原子处于n=5激发态时原子系统具有的能量为-0.54eV.
②电子在n=3轨道上运动的动能为1.5eV.
点评:解决本题的关键能够建立正确的物理模型,结合所学的规律进行求解.

练习册系列答案
相关题目
 (选做题,在22A、22B中选做一题,若两题全做,以22A的得分计入总分.)
(选做题,在22A、22B中选做一题,若两题全做,以22A的得分计入总分.)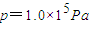 ,空气的平均摩尔质量M=2.9×10-2kg/mol,阿伏加德罗常数
,空气的平均摩尔质量M=2.9×10-2kg/mol,阿伏加德罗常数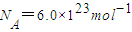 .
.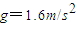 ,为开发月球的需要,设想在月球表面覆盖一层一定厚度的大气,若月球表面附近的大气压
,为开发月球的需要,设想在月球表面覆盖一层一定厚度的大气,若月球表面附近的大气压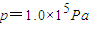 ,且已知大气层厚度比月球半径小得多,估算应给月球表面添加的大气层的总质量m.(保留一位有效数字)B、氢原于基态能量E1=-13.6eV,电子绕核做圆周运动的半径
,且已知大气层厚度比月球半径小得多,估算应给月球表面添加的大气层的总质量m.(保留一位有效数字)B、氢原于基态能量E1=-13.6eV,电子绕核做圆周运动的半径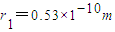 .求
.求