题目内容
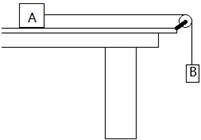
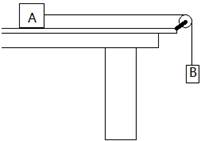
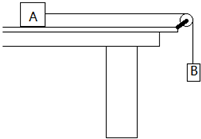如图所示，右端带滑轮的长木板放在水平桌面上，滑块A质量为M=2kg，连接滑块A和物体B的细线质量不计，与滑轮之间的摩擦不计，滑轮与A之间的细线沿水平方向，当B的质量为1kg时，A恰好不滑动（已知最大静摩擦力与滑动摩擦力相等），g取10m/s2，求当B的质量为1.75kg时：（1）A的加速度是多大？
（2）细线对滑轮的作用力．
分析：（1）当B的质量为1kg时，A恰好不滑动时，A所受摩擦力为Fμ=mBg=10N．当B的质量为1.75kg时，A向右匀加速运动，B向下匀加速运动，两者加速度大小相等，根据牛顿第二定律分别研究两个物体，求出加速度．
（2）细线对滑轮的作用力等于两绳拉力的合力，由平行四边形定则求解．
（2）细线对滑轮的作用力等于两绳拉力的合力，由平行四边形定则求解．
解答：解：（1）
由题意可知：A恰好不滑动时，所受摩擦力为Fμ=mBg=1×10N=10N
当B的质量为1.75kg时
对A：F-Fμ=Ma ①
对B：mg-F=ma ②
由①②得：a=2m/s2，F=14N
（2）细线对滑轮的作用力为F合=
=14
N
且tanα=
=1，得α=45°所以细线对滑轮的作用力大小为14
N，与竖直方向夹角为45°．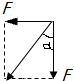
答：
（1）A的加速度是2m/s2．
（2）细线对滑轮的作用力大小为14
N，与竖直方向夹角为45°．
由题意可知：A恰好不滑动时，所受摩擦力为Fμ=mBg=1×10N=10N当B的质量为1.75kg时
对A：F-Fμ=Ma ①
对B：mg-F=ma ②
由①②得：a=2m/s2，F=14N
（2）细线对滑轮的作用力为F合=
| F2+F2 |
| 2 |
且tanα=
| F |
| F |
| 2 |
答：
（1）A的加速度是2m/s2．
（2）细线对滑轮的作用力大小为14
| 2 |
点评：本题采用隔离法研究连接体问题，也可以运用整体法进行解答，关键要抓住连接体的特点：加速度大小相等．
练习册系列答案
相关题目
