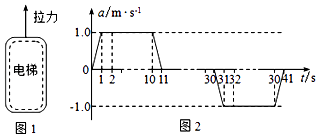
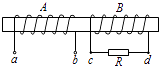
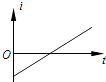
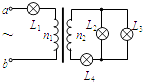题目内容
【题目】如图,三棱镜的横截面为直角三角形ABC,∠A=30°,AC平行于光屏MN,与光屏的距离为L.棱镜对红光的折射率为n1 , 对紫光的折射率为n2 . 一束很细的白光由棱镜的侧面AB垂直射入,直接到达AC面并射出.画出光路示意图,并标出红光和紫光射在光屏上的位置,求红光和紫光在光屏上的位置之间的距离.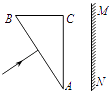
【答案】解:根据几何关系,光从AC面上折射时的入射角为30°,
根据折射定律有:![]() ,
, ![]()
则tanr2= ![]() ,tanr1=
,tanr1= ![]() .
.
所以x=L(tanr2﹣tanr1)= ![]() .
.
答:红光和紫光在光屏上的位置之间的距离 ![]()
【解析】两种色光组成的很细的光束垂直AB边射入棱镜,在AB面上不发生偏折,到达AC面上,根据几何关系求出入射角的大小,根据折射定律求出折射角,再根据几何关系求出光屏MN上两光点间的距离.
【考点精析】本题主要考查了光的折射的相关知识点,需要掌握光由一种介质射入另一种介质时,在两种介质的界面上将发生光的传播方向改变的现象叫光的折射才能正确解答此题.

练习册系列答案
相关题目