Question

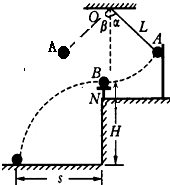
用如图所示装置来探究碰撞中的守恒量，质量为m_B的钢球B放在小支柱N上，球心离地面高度为H；质量为m_A的钢球A用细线拴好悬挂于O点，当细线被拉直时O点到球心的距离为L，细线与竖直线之间夹角α；A球由静止释放，摆到最低点时恰与B球发生正碰，碰撞后，A球摆到与竖直夹角为β处，B球落到地面上，地面上铺有一张盖有复写纸的白纸，用来记录球B的落点．
（1）用图中所示各个物理量的符号表示：碰撞前A球的速度V_A=______；碰撞后B球的速度V_B=______；此实验探究守恒量的最后等式为______
（2）请你提供一条提高实验精度的建议：______．

Answer 1

（1）A球下摆过程机械能守恒，根据机械能守恒定律得：
m_Agl（1-cosα）=

1

2

m

v

2A

解得：vA=

2gl(1-cosα)

碰撞后B球做平抛运动，根据平抛运动的分位移公式，有：
水平方向：s=v_Bt
竖直方向：H=

1

2

gt2
解得：V_B=s

g 2H

碰撞后A球向上摆动过程机械能守恒，根据机械能守恒定律得：
-m_Bgl（1-cosβ）=-

1

2

m

v

2B

解得：vA=

2gl(1-cosβ)

根据动量守恒定律，需验证：
m_A

2gl(1-cosα)

=m_A

2gl(1-cosβ

)+mBs

g 2H

（2）由于偶然误差，每次小球的落地点不同，可以采用：多次测落点取平均值．
故答案为：（1）

2gl(1-cosα)

，s

g 2H

，m_A

2gl(1-cosα)

=m_A

2gl(1-cosβ

)+mBs

g 2H

；（2）多次测落点取平均值．