题目内容
3.某同学在“探究小车运动速度随时间变化的规律”的实验中,用打点计时器记录被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻点间的距离如图a所示,每两个相邻的计数点之间的时间间隔为0.1s.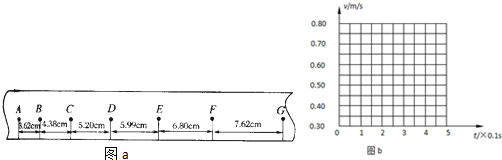
(1)试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入下式(要求保留三位有效数字)
vB=0.400m/s;vc=0.479m/s;vD=0.560m/s;vE=0.640m/s;vy=0.721m/s.
(2)若从纸带上打A点的时刻开始计时,将B、C、D、E、F各个时刻的瞬时速度在如图b所示的坐标纸上,并画出小车的瞬时速度随时间变化的关系图线.
(3)根据作出的图象计算小车的加速度.
分析 (1)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上B、C、D、E、F点时小车的瞬时速度大小.
(2)用描点法画出小车的瞬时速度随时间变化的关系图线.
(3)根据图象的斜率表示加速度求解.
解答 解:(1)相邻的计数点之间的时间间隔为0.1s,
利用匀变速直线运动的推论得,物体的瞬时速度:
vB=$\frac{{x}_{AC}}{2t}$=$\frac{0.0362+0.0438}{2×0.1}$=0.400m/s,
vC=$\frac{{x}_{BD}}{2t}$=$\frac{0.0438+0.0520}{2×0.1}$=0.479m/s,
vD=$\frac{{x}_{CE}}{2t}$=$\frac{0.0520+0.0599}{2×0.1}$=0.560m/s,
vE=$\frac{{x}_{DF}}{2t}$=$\frac{0.0599+0.0680}{2×0.1}$=0.640m/s,
vF=$\frac{{x}_{EG}}{2t}$=$\frac{0.0680+0.0762}{2×0.1}$=0.721m/s;
(2)将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线.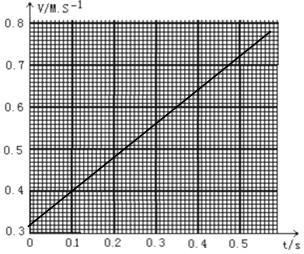
(3)根据v-t图象求出图形的斜率k,v-t图象斜率代表物体的加速度.所以小车加速度为:
a=k=$\frac{0.72-0.32}{0.5}$=0.80m/s2.
故答案为:(1)0.400;0.479;0.560;0.640;0.721;(2)图象如图所示;(3)小车的加速度为:0.80m/s2.
点评 要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.要注意单位的换算.

练习册系列答案
相关题目
14.汽车后刹车灯的光源,若采用发光二极管(LED),则通电后亮起的时间会比采用灯丝的白炽灯大约快0.5秒,故有助于后车驾驶员提前作出反应,假设后车以36km/h的车速匀速前进,则在0.5秒的时间内,后车前行的距离大约为多少米?( )
| A. | 3 | B. | 5 | C. | 7 | D. | 13 |
11.在公路的每个路段都有交管部门设置的限速标志如图所示,这是告诫驾驶员在这一路段驾驶车辆时( )


| A. | 平均速度的大小不得超过这一数值 | |
| B. | 必须一直以这一规定速度行驶 | |
| C. | 汽车上的速度指示数值,有时可以超过这一数值 | |
| D. | 瞬时速度的大小不得超过这一数值 |
18.下列说法中指时刻的是( )
| A. | 第2s内 | B. | 前2s内 | C. | 第5s初 | D. | 第6s末 |
8.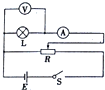 如图所示,某同学在做测小灯泡的伏安特性曲线的实验中闭合开关,将滑动变阻器的滑片P左右移动,发现“电流表的示数几乎为零,电压表的示数有明显变化”,则分析电路的可能故障为( )
如图所示,某同学在做测小灯泡的伏安特性曲线的实验中闭合开关,将滑动变阻器的滑片P左右移动,发现“电流表的示数几乎为零,电压表的示数有明显变化”,则分析电路的可能故障为( )
 如图所示,某同学在做测小灯泡的伏安特性曲线的实验中闭合开关,将滑动变阻器的滑片P左右移动,发现“电流表的示数几乎为零,电压表的示数有明显变化”,则分析电路的可能故障为( )
如图所示,某同学在做测小灯泡的伏安特性曲线的实验中闭合开关,将滑动变阻器的滑片P左右移动,发现“电流表的示数几乎为零,电压表的示数有明显变化”,则分析电路的可能故障为( )| A. | 小灯泡短路 | B. | 小灯泡断路 | C. | 电流表断路 | D. | 滑动变阻器断路 |
12. 将地面上静止的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图象如图所示.以下判断正确的是( )
将地面上静止的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图象如图所示.以下判断正确的是( )
 将地面上静止的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图象如图所示.以下判断正确的是( )
将地面上静止的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图象如图所示.以下判断正确的是( )| A. | 前3 s内货物处于超重状态 | |
| B. | 最后2 s内货物只受重力作用 | |
| C. | 前3 s内与最后4 s内货物的平均速度相同 | |
| D. | 第3 s末至第5 s末的过程中,货物的机械能守恒 |
13.如图所示,在同一直线上、由同一地点出发的甲、乙两物体的v-t图象,则由图象可知( )
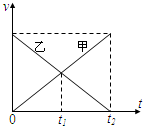

| A. | 它们速度方向相同,加速度方向相反 | |
| B. | 在t1时刻它们相距最远 | |
| C. | 在t1时刻它们相遇 | |
| D. | 在0~t2时间内它们的位移相同 |
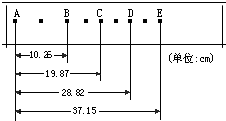 在“探究小车速度随时间变化规律”的实验中:
在“探究小车速度随时间变化规律”的实验中: