题目内容
①沿直线做匀加速运动的某物体,牵引一条通过打点计时器的纸带,计时器的打点周期T=0.02s,取下纸带后,由某一计时点开始,每隔五个点剪下一段纸带,按图1那样贴在直角坐标平面上,彼此不留间隙,也不要重叠.纸带下端都要准确地与横轴重合,每一条纸带的左边准确地与纵轴平行,图的纵轴上已标出了每条纸带的长度L(单位:mm).今以横轴为时间轴,令每条纸带的宽度代表一个时间单位:0.1s,以纵轴为速度轴,纵轴上原来标的每毫米代表一个速度单位:10mm/s.
(1)在每段纸带的上边缘中点画“?”作为计数点,在新的坐标里每个计数点的纵坐标表示______.
(2)画一直线,使尽可能多的计数点落在此直线上,并使直线两侧的计数点数目大致相等,这条直线便是运动物体的______图线.
(3)求出上述直线的斜率,可知运动物体的加速度a=______m/s2.
②在“探究加速度与力、质量的关系”的实验时:
(1)我们已经知道,物体的加速度(a)同时跟合外力(F)和质量(m)两个因素有关.要研究这三个物理量之间的定量关系的基本思路是______
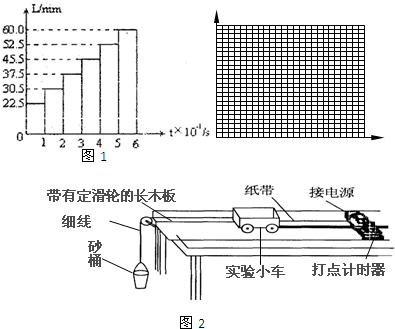
(2)某同学的实验方案如图2所示,她想用砂和砂桶的重力表示小车受到的合外力,为了减少这种做法而带来的实验误差,你认为在实验中还应该采取的两项措施是:a.______;b.______.
(3)该同学利用实验中打出的纸带求加速度时,处理方案有两种:
A、利用公式a=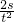 计算;B、根据a=
计算;B、根据a=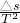 利用逐差法计算.
利用逐差法计算.
两种方案中,你认为选择方案______比较合理.
(4)下表是该同学在探究“保持m不变,a与F的关系”时记录的一组实验数据,请你根据表格中的数据在下面的坐标系中做出a-F图象;
( 小车质量:M=0.500kg,g=10m/s2 )
| 次数 物理量 | 1 | 2 | 3 | 4 | 5 | 6 |
| m砂和桶(kg) | 0.010 | 0.020 | 0.030 | 0.040 | 0.050 | 0.060 |
| a(m/s2) | 0.196 | 0.390 | 0.718 | 0.784 | 0.990 | 1.176 |
解:①(1)因为剪断的纸带所用的时间都是t=0.1s,即时间t相等,所以纸带的长度之比等于此段纸带的平均速度之比;而此段纸带的平均速度等于这段纸带中间时刻的速度,最后得出结论纸带的长度之比等于此段纸带的平均速度之比,还等于各段纸带中间时刻的速度之比,即纸带的高度之比等于中间时刻速度之比.在每段纸带的上边缘中点画“?”作为计数点,在新的坐标里每个计数点的纵坐标表示相对应的单位时间内中间时刻的瞬时速度.
(2)画一直线,使尽可能多的计数点落在此直线上,并使直线两侧的计数点数目大致相等,这条直线便是运动物体的速度-时间 图线.
(3)速度-时间直线的斜率表示加速度,可知运动物体的加速度a=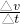 =0.75m/s2.
=0.75m/s2.
②(1)我们已经知道,物体的加速度(a)同时跟合外力(F)和质量(m)两个因素有关.要研究这三个物理量之间的定量关系的基本思路是运用控制变量法,即先保持m不变,研究a与F的关系;再保持F不变,研究a与m的关系;
(2)某同学的实验方案如图2所示,她想用砂和砂桶的重力表示小车受到的合外力,由于保持F不变,研究a与M的关系.则当质量发生改变时,若没有平衡摩擦力,则砂桶的重力就不再是小车所受的合力,所以必须平衡摩擦力.由于小车的加速运动,出现加速度,所以导致砂桶的重力大于拉小车的细线的拉力.当砂桶的质量远小于小车的质量时,砂桶的重力接近拉小车的细线的拉力.为了减少这种做法而带来的实验误差,在实验中还应该采取的两项措施是:
a.把木板的末端垫起适当高度以平衡摩擦力;b.砂和桶的质量远小于小车质量;
(3)由于做匀变速直线的物体在相等的时间内位移总是相等.所以可借助于a= 利用逐差法计算加速度大小.故选B.
利用逐差法计算加速度大小.故选B.
(4)在坐标系中做出a-F图象:
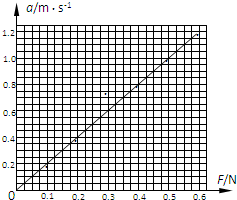 (5)针对该同学的实验设计、实验操作、数据采集与处理,就其中的某一环节,有别于该同学的设计或处理方法:
(5)针对该同学的实验设计、实验操作、数据采集与处理,就其中的某一环节,有别于该同学的设计或处理方法:
①采用气垫导轨以减小摩擦力;
②利用“光电门”和计算机连接直接得到加速度,
③利用v-t图象计算加速度;
④用弹簧秤测量砂和桶的重力;
⑤用力和加速度的比值是否不变来处理数据,等等.
故答案为:①(1)相对应的单位时间内中间时刻的瞬时速度
(2)速度-时间 (3)0.75m/s2
②(1)先保持m不变,研究a与F的关系;再保持F不变,研究a与m的关系;
(2)a.把木板的末端垫起适当高度以平衡摩擦力;b.砂和桶的质量远小于小车质
量;
(3)B;(4)如图,(5)①采用气垫导轨以减小摩擦力;
②利用“光电门”和计算机连接直接得到加速度,
③利用v-t图象计算加速度;
④用弹簧秤测量砂和桶的重力;
⑤用力和加速度的比值是否不变来处理数据,等等.
分析:(1)本题使用的方法是等效代替法解题,它们的长度分别等于x=v平均t,因为剪断的纸带所用的时间都是t=0.1s,即时间t相等,所以纸带的长度之比等于此段纸带的平均速度之比;而此段纸带的平均速度等于这段纸带中间时刻的速度,最后得出结论纸带的长度之比等于此段纸带的平均速度之比,还等于各段纸带中间时刻的速度之比,即纸带的高度之比等于中间时刻速度之比.根据图象的斜率求出小车的加速度.
(2)当一个量与多个量有关系时,则可控制某些量不变,去研究另两个量的关系;再去改变让其它量不变,则再去研究剩余的两个量关系,例如:先保持M不变,研究a与F的关系;再保持F不变,研究a与M的关系.
在实验中,为了减少这种做法而带来的实验误差,一要排除摩擦力的影响,二要砂桶的重力接近小车所受的合力.
由于做匀变速直线的物体在相等的时间内位移总是相等.所以可借助于a= 利用逐差法计算加速度大小.
利用逐差法计算加速度大小.
点评:(1)要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.
(2)由牛顿第二可得,当小车的质量远大于砂桶的质量时,砂桶的重力就约等于小车的合力.
由加速度与合力的图象可知,斜率的大小表示物体的质量大小,若图线与纵轴有交点时,则说明摩擦力没有平衡或没有平衡彻底;若图线与横轴有交点时,则说明摩擦力平衡过度.
(2)画一直线,使尽可能多的计数点落在此直线上,并使直线两侧的计数点数目大致相等,这条直线便是运动物体的速度-时间 图线.
(3)速度-时间直线的斜率表示加速度,可知运动物体的加速度a=
 =0.75m/s2.
=0.75m/s2.②(1)我们已经知道,物体的加速度(a)同时跟合外力(F)和质量(m)两个因素有关.要研究这三个物理量之间的定量关系的基本思路是运用控制变量法,即先保持m不变,研究a与F的关系;再保持F不变,研究a与m的关系;
(2)某同学的实验方案如图2所示,她想用砂和砂桶的重力表示小车受到的合外力,由于保持F不变,研究a与M的关系.则当质量发生改变时,若没有平衡摩擦力,则砂桶的重力就不再是小车所受的合力,所以必须平衡摩擦力.由于小车的加速运动,出现加速度,所以导致砂桶的重力大于拉小车的细线的拉力.当砂桶的质量远小于小车的质量时,砂桶的重力接近拉小车的细线的拉力.为了减少这种做法而带来的实验误差,在实验中还应该采取的两项措施是:
a.把木板的末端垫起适当高度以平衡摩擦力;b.砂和桶的质量远小于小车质量;
(3)由于做匀变速直线的物体在相等的时间内位移总是相等.所以可借助于a=
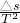 利用逐差法计算加速度大小.故选B.
利用逐差法计算加速度大小.故选B.(4)在坐标系中做出a-F图象:
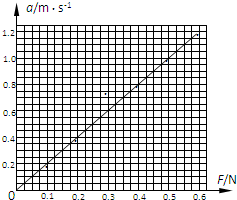 (5)针对该同学的实验设计、实验操作、数据采集与处理,就其中的某一环节,有别于该同学的设计或处理方法:
(5)针对该同学的实验设计、实验操作、数据采集与处理,就其中的某一环节,有别于该同学的设计或处理方法:①采用气垫导轨以减小摩擦力;
②利用“光电门”和计算机连接直接得到加速度,
③利用v-t图象计算加速度;
④用弹簧秤测量砂和桶的重力;
⑤用力和加速度的比值是否不变来处理数据,等等.
故答案为:①(1)相对应的单位时间内中间时刻的瞬时速度
(2)速度-时间 (3)0.75m/s2
②(1)先保持m不变,研究a与F的关系;再保持F不变,研究a与m的关系;
(2)a.把木板的末端垫起适当高度以平衡摩擦力;b.砂和桶的质量远小于小车质
量;
(3)B;(4)如图,(5)①采用气垫导轨以减小摩擦力;
②利用“光电门”和计算机连接直接得到加速度,
③利用v-t图象计算加速度;
④用弹簧秤测量砂和桶的重力;
⑤用力和加速度的比值是否不变来处理数据,等等.
分析:(1)本题使用的方法是等效代替法解题,它们的长度分别等于x=v平均t,因为剪断的纸带所用的时间都是t=0.1s,即时间t相等,所以纸带的长度之比等于此段纸带的平均速度之比;而此段纸带的平均速度等于这段纸带中间时刻的速度,最后得出结论纸带的长度之比等于此段纸带的平均速度之比,还等于各段纸带中间时刻的速度之比,即纸带的高度之比等于中间时刻速度之比.根据图象的斜率求出小车的加速度.
(2)当一个量与多个量有关系时,则可控制某些量不变,去研究另两个量的关系;再去改变让其它量不变,则再去研究剩余的两个量关系,例如:先保持M不变,研究a与F的关系;再保持F不变,研究a与M的关系.
在实验中,为了减少这种做法而带来的实验误差,一要排除摩擦力的影响,二要砂桶的重力接近小车所受的合力.
由于做匀变速直线的物体在相等的时间内位移总是相等.所以可借助于a=
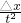 利用逐差法计算加速度大小.
利用逐差法计算加速度大小.点评:(1)要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.
(2)由牛顿第二可得,当小车的质量远大于砂桶的质量时,砂桶的重力就约等于小车的合力.
由加速度与合力的图象可知,斜率的大小表示物体的质量大小,若图线与纵轴有交点时,则说明摩擦力没有平衡或没有平衡彻底;若图线与横轴有交点时,则说明摩擦力平衡过度.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 (2011?皇姑区一模)在现代科技中,人们常常利用电场、磁场和重力场来控制带电微粒的运动.如图所示,直角坐标系位于竖直面内,y轴上的A点有一带正电的小球,小球的质量为m、电量为q,
(2011?皇姑区一模)在现代科技中,人们常常利用电场、磁场和重力场来控制带电微粒的运动.如图所示,直角坐标系位于竖直面内,y轴上的A点有一带正电的小球,小球的质量为m、电量为q,