题目内容
小玉所在的学习小组在研究了“嫦娥一号”相关报道后得知,绕月卫星在完成其绕月的伟大历史使命后,最终将通过撞击月球表面完成最后的多项科学使命,对此同学们做了相关的研究并提出了相应的问题.
(1)“嫦娥一号”探月卫星执行的一项重要任务就是评估月壤中氦-3的分布和储量.两个氘核聚变生成一个氦-3的核反应方程是:2
H→
He+ +3.26MeV,请在横线上写出相应粒子的符号.
(2)同学们提出若“嫦娥一号”以速率v竖直撞击月球后,可弹回到距月球表面大约为h的高度,设此过程动能损失了50%,则由此可推算出月球表面的重力加速度g′多大?
(3)设月球半径约为地球半径的1/4,月球的质量约为地球质量的1/81,不考虑月球自转的影响,在月球上要发射一颗环月卫星,则最小发射速度多大?(地表处的重力加速度g取10m/s2,地球半径R=6400km,计算结果保留两位有效数字)
(1)“嫦娥一号”探月卫星执行的一项重要任务就是评估月壤中氦-3的分布和储量.两个氘核聚变生成一个氦-3的核反应方程是:2
2 1 |
3 2 |
(2)同学们提出若“嫦娥一号”以速率v竖直撞击月球后,可弹回到距月球表面大约为h的高度,设此过程动能损失了50%,则由此可推算出月球表面的重力加速度g′多大?
(3)设月球半径约为地球半径的1/4,月球的质量约为地球质量的1/81,不考虑月球自转的影响,在月球上要发射一颗环月卫星,则最小发射速度多大?(地表处的重力加速度g取10m/s2,地球半径R=6400km,计算结果保留两位有效数字)
分析:(1)根据参与反应的粒子种类及生成粒子的种类,根据质量数守恒与核电荷数守恒写出核反应方程式.
(2)根据机械能守恒定律列式即可求解;
(3)先求出地球发射卫星的最小发射速度,通过类比即可求解.
(2)根据机械能守恒定律列式即可求解;
(3)先求出地球发射卫星的最小发射速度,通过类比即可求解.
解答:解:(1)核反应方程是2
H→
He+
n+3.26MeV,
(2)设竖直弹回的速度大小为v2,则:
m
=
mv2×50%
由机械能守恒定律可得:
m
=mg′h
两式联立解得:g′=
(3)设地球、月球质量分别为M1、M2,地球、月球半径分别为R1、R2,卫星质量为m,在地球、月球上发射卫星的最小速度分别为v1、v2.
在地球表面附近,mg=m
最小发射速度v1=
=
m/s=8km/s
对地球近地卫星,根据万有引力定律有G
=m
①
对月球近地卫星,根据万有引力定律有G
=m
②
解①②两式得v2=
v1=
×8km/s=1.8km/s
答:(1)
n;(2)月球表面的重力加速度g′为
;(3)在月球上发射一颗环月卫星,最小发射速度为1.8km/s.
2 1 |
3 2 |
1 0 |
(2)设竖直弹回的速度大小为v2,则:
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
由机械能守恒定律可得:
| 1 |
| 2 |
| v | 2 2 |
两式联立解得:g′=
| v2 |
| 4h |
(3)设地球、月球质量分别为M1、M2,地球、月球半径分别为R1、R2,卫星质量为m,在地球、月球上发射卫星的最小速度分别为v1、v2.
在地球表面附近,mg=m
| ||
| R1 |
最小发射速度v1=
| gR1 |
| 10×6400×103 |
对地球近地卫星,根据万有引力定律有G
| M1m | ||
|
| ||
| R1 |
对月球近地卫星,根据万有引力定律有G
| M2m | ||
|
| ||
| R2 |
解①②两式得v2=
|
|
答:(1)
1 0 |
| v2 |
| 4h |
点评:本题考查原子核反应方程、机械能守恒定律、万有引力定律、牛顿第二定律等知识.考查理解能力、综合分析能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
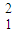 H→
H→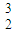 He+______n
He+______n