Question

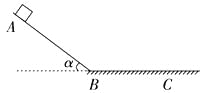
【题目】如图所示，一固定光滑杆与水平方向夹角为θ，将一质量为m1的小环套在杆上，通过轻绳悬挂一个质量为m2的小球，由静止释放后，小环与小球保持相对静止并以相同的加速度a一起下滑，此时轻绳与竖直方向的夹角为β，则下列说法正确的是（ ）

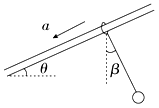
A．a＝gsinθ

B．m1不变，则m2越大，β越小

C．θ＝β，且与m1、m2无关

D．杆对小环的作用力大小大于m1g＋m2g

Answer 1

【答案】AC

【解析】

试题分析：对小球研究可知，其合力大小为F=m2gsinθ，等于重力沿杆向下方向的分力，则细线与杆垂直，则由几何知识得，θ=β，与环和小球的质量无关，故B错误，C正确；若杆不光滑；把环和球看做一个整体受力分析，沿斜面和垂直斜面建立直角坐标系得：

沿斜面方向：（m1+m2）gsinθ-f=（m1+m2）a

垂直斜面方向：FN=（m1+m2）gcosθ

摩擦力：f=μFN

联立可解得：a=gsinθ-μgcosθ，

设θ=β，由几何关系知，此时绳应该和杆垂直，对小球受力分析可知重力沿杆的分力作为合力产生加速度，

垂直于杆的分力与绳的拉力相平衡，此时可以求得小球的加速度为gsinθ，故A正确；以整体为研究对象，根据牛顿第二定律得：（m1+m2）gsinθ=（m1+m2）a

得：a=gsinθ

N=（m1+m2）gcosθ＜（m1+m2）g；故D错误；故选AC．