Question

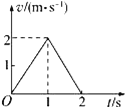
【题目】如图为固定在竖直平面内的轨道，直轨道AB与光滑圆弧轨道 BC相切，圆弧轨道的圆心角为37°，半径为r=0.25m，C端水平, AB段的动摩擦因数为0.5．竖直墙壁CD高H=0.2m,紧靠墙壁在地面上固定一个和CD等高，底边长L=0.3m的斜面．一个质量m=0.1kg的小物块(视为质点)在倾斜轨道上从距离B点l=0.5m处由静止释放，从C点水平抛出．重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8．求：

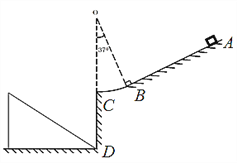
(1)小物块运动到C点时对轨道的压力的大小；

(2)小物块从C点抛出到击中斜面的时间；

(3)改变小物体从轨道上释放的初位置，求小物体击中斜面时动能的最小值．

Answer 1

【答案】（1）2.2N（2）（3）0.15;

【解析】试题分析：（1）

得：

，,

由牛顿第三定律得,压力为2.2N

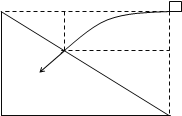
(2)如图，设物体落到斜面上时水平位移为x,竖直位移为y,

，

，，

，

（3），

解得：当y=0.12m，