题目内容
【题目】如图,两个小滑块A和B分别置于静止在水平地面上的木板C的两端,A、B和C三者质量相等,A、B与C间的动摩擦因数均为1=0.5,木板C与地面间的动摩擦因数为2=0.2。某时刻,A、B两滑块分别以速度vA=7m/s、vB=2m/s开始相向滑动,当A、B相遇吋,B的速度恰好为零,A、B相遇后,两者瞬间粘在一起继续运动。设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2,求:

(1)A、B相遇前的瞬间,A的速度大小;
(2)通过计算判断A、B粘在一起后是否会脱离木板C;
(3)当三者相对地面静止时,木板C滑行的总距离。
【答案】(1) ![]() (2) 不会脱离C板 (3)
(2) 不会脱离C板 (3) ![]()
【解析】(1)开始C物体静止,AB的加速度为: ![]() ①
①
![]() ②,
②,![]() ③
③
由①②③得: ![]()
(2)由动量守恒得: ![]() ④
④
设ABC速度相同时为v,则有: ![]() ⑤,
⑤,![]() ⑥
⑥
由C的受力,由牛顿第二定律得: ![]() ⑦
⑦
![]() ⑧,
⑧,![]() ⑨
⑨
由④⑤⑥⑦⑧⑨得: ![]()
解得: ![]()
由![]() 得:不会脱离C板
得:不会脱离C板
(3)ABC共速之后,以ABC为整体得: ![]() ,
, ![]()
C共滑行的距离为: ![]()

【题目】某多用电表内欧姆挡“x1”的内部电路图如图所示,小明同学将电阻筘和电压表V并联后接在两表笔a、b上,欲用图示的电路测量多用电表内部的电阻r(远小于电压表V的内阻)和电池的电动势E。实验的主要步骤为:
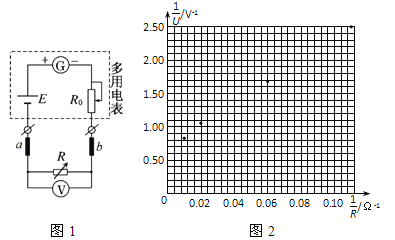
(2)表笔a为(填“红表笔,或“黑表笔”)。将选择开关转至欧姆挡“x1”,将红黑表笔短接,调节_________,使指针指在_________.(填“左”或“右”)侧零刻度处。
(2)改变电阻箱R的阻值,分别读出6组电压表和电阻箱的示数U、R,将![]() 的值算出并记录在表格中,请将第3、5组数据的对应点在坐标纸上补充标出,并作出
的值算出并记录在表格中,请将第3、5组数据的对应点在坐标纸上补充标出,并作出![]() 图线_____。
图线_____。
组数 | 1 | 2 | 3 | 4 | 5 | 6 |
R | 100.0 | 50.0 | 25.0 | 16.7 | 12.5 | 9.1 |
| 0.01 | 0.02 | 0.04 | 0.06 | 0.08 | 0.11 |
U | 1.20 | 0.95 | 0.74 | 0.60 | 0.50 | 0.40 |
| 0.83 | 1.05 | 1.35 | 1.68 | 2.00 | 2.50 |
根据图线得到电动势E=_____V,内电阻r=_____Ω(结果保留三位有效数字)
由于电压表的分流作用,多用电表内部电池的电动势的测量值比真实值_______(填“大”或“小”)。