题目内容
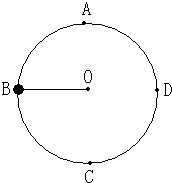 如图所示,长为0.9m的细绳一端固定于O点,另一端拴一质量为0.9kg的小球.小球在竖直平面内做圆周运动.(取g=10m/s2)
如图所示,长为0.9m的细绳一端固定于O点,另一端拴一质量为0.9kg的小球.小球在竖直平面内做圆周运动.(取g=10m/s2)(1)小球运动中通过何处的速度最小?要做完整圆周运动,小球通过该点的最小速度是多少?
(2)小球通过何处时对绳的拉力最大?若绳能承受的最大拉力为90N,要避免绳被拉断,小球通过该点的最大速度是多少?
分析:小球做圆周运动,只有重力做功,机械能守恒,合外力提供向心力,根据向心力公式及机械能守恒定律列方程即可求解.
解答:解:(1)小球做圆周运动,只有重力做功,机械能守恒,重力势能越大,速度越小,所以在A点速度最小
要做完整圆周运动,在A点当重力提供向心力时,速度最小,则有:
mg=m
解得:v=
=3m/s
(2)在C点重力势能最小,所以在C点速度最大,此时需要的向心力也最大,则有:
T-mg=m
解得:v′=
当T=90N时,速度最大,所以最大速度v′=
=9m/s
答:(1)小球运动中通过A处的速度最小,要做完整圆周运动,小球通过该点的最小速度是3m/s;
(2)小球通过C处时对绳的拉力最大,若绳能承受的最大拉力为90N,要避免绳被拉断,小球通过该点的最大速度是9m/s.
要做完整圆周运动,在A点当重力提供向心力时,速度最小,则有:
mg=m
| v2 |
| r |
解得:v=
| gr |
(2)在C点重力势能最小,所以在C点速度最大,此时需要的向心力也最大,则有:
T-mg=m
| v′2 |
| r |
解得:v′=
|
当T=90N时,速度最大,所以最大速度v′=
|
答:(1)小球运动中通过A处的速度最小,要做完整圆周运动,小球通过该点的最小速度是3m/s;
(2)小球通过C处时对绳的拉力最大,若绳能承受的最大拉力为90N,要避免绳被拉断,小球通过该点的最大速度是9m/s.
点评:解决本题的关键知道小球做圆周运动向心力的来源,知道“绳模型”最高点的临界情况,结合牛顿第二定律进行分析.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 (2011?厦门模拟)[物理--选修3-5]
(2011?厦门模拟)[物理--选修3-5]

 如图所示,长L=0. 4 m的两平行金属板A、B竖直放置,相距d=0. 02 m,两板间接入恒定电压为182 V且B板接正极一电子质量m=9. 1
如图所示,长L=0. 4 m的两平行金属板A、B竖直放置,相距d=0. 02 m,两板间接入恒定电压为182 V且B板接正极一电子质量m=9. 1