题目内容
4．一横截面积为S的铜导线，流经其中的电流为I，设单位体积的导线中有n个自由电子，电子的电荷量为q．此时电子的定向移动速度为v，在t时间内，通过铜导线横截面的自由电子数目可表示为（ ）| A． | nqvSt | B． | nvt | C． | $\frac{It}{q}$ | D． | $\frac{It}{Sq}$ |
分析 根据电流的两个表达式来分析，首先从导体导电的微观角度来说，在t时间内能通过某一横截面的自由电子必须处于长度为vt的圆柱体内，由于自由电子可以认为是均匀分布，故此圆柱体内的电子数目为nvSt．而从电流的定义来说，I=$\frac{q}{t}$，故在t时间内通过某一横截面的电荷量为It，通过横截面的自由电子数目为$\frac{It}{q}$．
解答 解：A、从微观角度来说，在t时间内能通过某一横截面的自由电子必须处于长度为vt的圆柱体内，此圆柱体内的电子数目为nvSt，所以nqvSt是长度为vt的铜导线内的自由电荷的电量．故A错误；
B、由于vt是电子通过的距离，nvt没意义，缺少面积s，故B错误；
C、从电流的定义式来说，I=$\frac{q}{t}$，故在t时间内通过某一横截面的电荷量为It，通过横截面的自由电子数目为$\frac{It}{q}$，故C正确；
D、$\frac{It}{qs}$是通过铜导线单位横截面的自由电子数，故D错误；
故选：C．
点评 本题考查了电流的两个表达式，在解答的过程中，不需要推导公式I=neSv，但要特别注意微观表达式I=nevS中各物理量的意义．
练习册系列答案
相关题目
14．如图是站在水平地面上的女孩手拿瓶举在空中，下列说法正确的是（ ）
| A． | 瓶子受到的弹力等于重力 | |
| B． | 由于瓶子静止，可能不受摩擦力作用 | |
| C． | 瓶子可能没有发生形变 | |
| D． | 瓶子侧壁一定不光滑 |
15．运动员在110m栏项目中，以11.00s的成绩夺得金牌，并打破了奥运会纪录，假定他在起跑后10m处的速度是8.0m/s，到达终点时的速度是9.6m/s，则他在全程中的平均速度为（ ）
| A． | 8.0m/s | B． | 9.6m/s | C． | 8.8m/s | D． | 10m/s |
小明在联系使用多用电表时应将黑表笔插入多用电表的-（填“+”、“-”）插孔，多用电表的电阻挡有四个倍率，分别是×1、×10、×100、×1k．用×100挡测量某电阻时，操作步骤正确，发现表头指针偏转角度很小，为了较准确地进行测量，应换到×1k挡．如果换挡后立即用表笔连接待测电阻进行读数，那么缺少的步骤是欧姆调零，若补上该步骤后测量，表盘的示数如图，则该电阻的阻值为12kΩ．
19．
倾角为θ的粗糙斜面上放一质量为m的木块，接触面间的动摩擦因数为μ，现通过一轻质定滑轮沿斜面向上拉木块，拉力的功率恒为P，斜面足够长，则木块可以获得的最大速度为（ ）
倾角为θ的粗糙斜面上放一质量为m的木块，接触面间的动摩擦因数为μ，现通过一轻质定滑轮沿斜面向上拉木块，拉力的功率恒为P，斜面足够长，则木块可以获得的最大速度为（ ）| A． | $\frac{P}{2（mgsinθ+μmgcosθ）}$ | B． | $\frac{2P}{mgsinθ+μmgcosθ}$ | ||
| C． | $\frac{P}{mgsinθ}$ | D． | $\frac{P}{mgsinθ+μmgcosθ}$ |
9．一个初速度为v0的物体沿直线运动，它的加速度方向和v0方向相同，且加速度a越来越大，t s后末速度为vt，则t s内物体平均速度v的大小满足（ ）
| A． | $\overline v=\frac{v_t^2-v_0^2}{2at}$ | B． | $\overline{v}$＜$\frac{{v}_{0}+{v}_{t}}{2}$ | ||
| C． | $\overline{v}$＞$\frac{{v}_{0}+{v}_{t}}{2}$ | D． | $\overline{v}$=$\frac{{v}_{0}+{v}_{t}}{2}$ |
13．
如图所示，平行板电容器与电动势为E的直流电源连接，上极板A接地．一带负电油滴固定于电容器中的P点．现将平行板电容器的下极板B竖直向下移动一小段距离，则（ ）
如图所示，平行板电容器与电动势为E的直流电源连接，上极板A接地．一带负电油滴固定于电容器中的P点．现将平行板电容器的下极板B竖直向下移动一小段距离，则（ ）| A． | P点的电势将升高 | B． | 电容器的极板带电量将减少 | ||
| C． | 带电油滴所受电场力不变 | D． | 带电油滴的电势能将增大 |
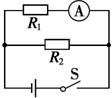如图电路中，R1=10Ω，R2=20Ω，闭合开关后，电流表（内阻不计）的示数为0.3A．