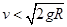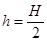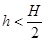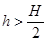题目内容
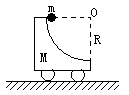
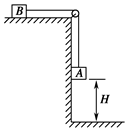
如图所示,半径R=0.40m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.10kg的小球,以初速度v0=7.0m/s在水平地面上向左做加速度a=3.0m/s2的匀减速直线运动,运动4.0m后,冲上竖直半圆环,最后小球落在C点.求A、C间的距离. (取重力加速度g=10m/s2)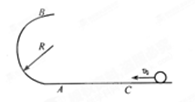

1.2m
【错解分析】不能求出小球到达圆环最高点B的速度而错。不能分析小球恰好做圆周运动的条件。
【正解】匀速速运动过程中,有:
 ①
①恰好做圆周运动时物体在最高点B满足:
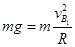
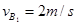 ②
②假设物体能达到圆环的最高点g,由机械能守恒:
 ③
③联立①③可得
vb="3" m/s
因为vB>vB1,所以小球能通过最高点B.
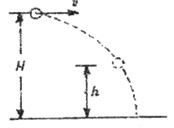
小球从及点做平抛运动,有:
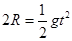 ④
④SAC=vB·t ⑤
由④⑤得SAC=1.2m

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
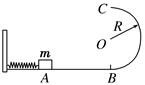
 ,仍要使物体恰能完成BC导轨上的圆周运动,则弹簧开始时的弹性势能至少为多少。
,仍要使物体恰能完成BC导轨上的圆周运动,则弹簧开始时的弹性势能至少为多少。 ,不计一切摩擦,下列说法中正确的是( )
,不计一切摩擦,下列说法中正确的是( )