题目内容
15. 如图,质量m=20kg的物块(可视为质点),以初速度v0=10m/s滑上静止在光滑轨道的质量M=30kg、高h=0.8m的小车的左端,当车向右运动了距离d时(即A处)双方达到共速.现在A处固定一高h=0.8m、宽度不计的障碍物,当车撞到障碍物时被粘住不动,而货物继续在车上滑动,到A处时即做平抛运动,恰好与倾角为53°的光滑斜面相切而沿斜面向下滑动,已知货物与车间的动摩擦因数μ=0.5,(g=10m/s2,sin53°=0.8,cos53°=0.6)求:
如图,质量m=20kg的物块(可视为质点),以初速度v0=10m/s滑上静止在光滑轨道的质量M=30kg、高h=0.8m的小车的左端,当车向右运动了距离d时(即A处)双方达到共速.现在A处固定一高h=0.8m、宽度不计的障碍物,当车撞到障碍物时被粘住不动,而货物继续在车上滑动,到A处时即做平抛运动,恰好与倾角为53°的光滑斜面相切而沿斜面向下滑动,已知货物与车间的动摩擦因数μ=0.5,(g=10m/s2,sin53°=0.8,cos53°=0.6)求:(1)车与货物共同速度的大小v1;
(2)货物平抛时的水平速度v2;
(3)车的长度L与距离d.
分析 (1)货物与车组成的系统动量守恒,应用动量守恒定律可以求出共同速度;
(2)货物离开车后做平抛运动,应用平抛运动规律可以求出货物抛出时的速度;
(3)应用动能定理可以求出车的长度与距离d.
解答 解:(1)车与货物已经到达共同速度,系统动量守恒,以向右为正方向,由动量守恒定律得:
mv0=(m+M)v1,
代入数据解得:v1=4m/s;
(2)货物从小车上滑出之后做平抛运动,竖直方向:h=$\frac{1}{2}$gt2,
代入数据解得:t=0.4s,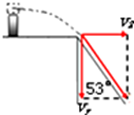
经过斜面顶点时,竖直分速度:
vy=gt=10×0.4m/s=4m/s,
tan53°=$\frac{{v}_{y}}{{v}_{2}}$,
解得:v2=$\frac{{v}_{y}}{tan53°}$=3m/s;
(3)对车,由动能定理得:μmgd=$\frac{1}{2}$Mv12-0,
代入数据解得:d=2.4m,
对货物,由动能定理得:-μmg(L+d)=$\frac{1}{2}$mv22-$\frac{1}{2}$mv02,
代入数据解得:L=6.7m;
答:(1)车与货物共同速度的大小v1为4m/s;
(2)货物平抛时的水平速度v2为3m/s;
(3)车的长度L为6.7m,距离d为2.4m.
点评 本题是一道力学综合题,考查了动量守恒定律与动能定理的应用,分析清楚物体运动过程是正确解题的关键,应用动量守恒定律、平抛运动规律与动能定理可以解题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6. 蹦床比赛中运动员与床垫接触的过程可简化为以下模型:如图所示,运动员从高处落到处于自然状态的床垫(A位置)上,随床垫一同向下运动到最低点(B位置).对于运动员从A位置运动到B位置的过程,下列说法正确的是( )
蹦床比赛中运动员与床垫接触的过程可简化为以下模型:如图所示,运动员从高处落到处于自然状态的床垫(A位置)上,随床垫一同向下运动到最低点(B位置).对于运动员从A位置运动到B位置的过程,下列说法正确的是( )
 蹦床比赛中运动员与床垫接触的过程可简化为以下模型:如图所示,运动员从高处落到处于自然状态的床垫(A位置)上,随床垫一同向下运动到最低点(B位置).对于运动员从A位置运动到B位置的过程,下列说法正确的是( )
蹦床比赛中运动员与床垫接触的过程可简化为以下模型:如图所示,运动员从高处落到处于自然状态的床垫(A位置)上,随床垫一同向下运动到最低点(B位置).对于运动员从A位置运动到B位置的过程,下列说法正确的是( )| A. | 运动员的机械能守恒 | |
| B. | 运动员的动能先增大后减小 | |
| C. | 在这个过程中,运动员受到的合力做了负功 | |
| D. | 运动员所受重力的瞬时功率一直在减小 |
6.从空中下落的物体,不考虑空气阻力,如果下落过程中某时刻重力突然消失,物体的运动情况将是( )
| A. | 悬浮在空中不动 | B. | 速度逐渐减小 | ||
| C. | 保持一定速度向下做匀速直线运动 | D. | 物体将向上运动 |
3.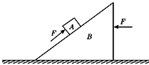 如图,在水平地面上有一质量为M的三角形斜面体B,质量为m的木块A置于B上,现用大小为F、方向沿斜面向上的力推A,同时用大小也为F、方向水平向左的力推B,它们均静止不动,则( )
如图,在水平地面上有一质量为M的三角形斜面体B,质量为m的木块A置于B上,现用大小为F、方向沿斜面向上的力推A,同时用大小也为F、方向水平向左的力推B,它们均静止不动,则( )
 如图,在水平地面上有一质量为M的三角形斜面体B,质量为m的木块A置于B上,现用大小为F、方向沿斜面向上的力推A,同时用大小也为F、方向水平向左的力推B,它们均静止不动,则( )
如图,在水平地面上有一质量为M的三角形斜面体B,质量为m的木块A置于B上,现用大小为F、方向沿斜面向上的力推A,同时用大小也为F、方向水平向左的力推B,它们均静止不动,则( )| A. | A与B之间一定存在摩擦力 | B. | B与地之间可能存在摩擦力 | ||
| C. | F一定大于mg | D. | 地面对B的支持力一定小于(M+m)g |
10. 如图所示,一质量为M的斜面静止在水平地面上,物体B受沿斜面向上力F作用沿斜面匀速上滑,A、B之间动摩擦因数为μ,μ<tanθ,且质量均为m,则( )
如图所示,一质量为M的斜面静止在水平地面上,物体B受沿斜面向上力F作用沿斜面匀速上滑,A、B之间动摩擦因数为μ,μ<tanθ,且质量均为m,则( )
 如图所示,一质量为M的斜面静止在水平地面上,物体B受沿斜面向上力F作用沿斜面匀速上滑,A、B之间动摩擦因数为μ,μ<tanθ,且质量均为m,则( )
如图所示,一质量为M的斜面静止在水平地面上,物体B受沿斜面向上力F作用沿斜面匀速上滑,A、B之间动摩擦因数为μ,μ<tanθ,且质量均为m,则( )| A. | A、B保持相对静止 | |
| B. | 地面对斜面体的摩擦力等于mg(sinθ-μcosθ)cosθ+Fcosθ | |
| C. | 地面受到的压力等于(M+2m)g | |
| D. | B与斜面间动摩擦因数为$\frac{F-mgsinθ-μmgcosθ}{2mgcosθ}$ |
20.关于电流,下列说法正确的是( )
| A. | 根据I=$\frac{q}{t}$可知,I一定与q成正比与t成反比 | |
| B. | 因为电流有方向,所以是矢量 | |
| C. | 任何相等时间内通过导体横截面的电量相等,则通过导体的电流一定是稳恒电流 | |
| D. | 电流的单位“安培”是国际单位中的基本单位 |
5.下列图象中,表示质点一直做匀加速直线运动的是( )
| A. |  | B. | 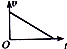 | C. | 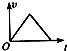 | D. |  |
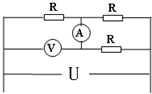 如图所示的电路中,三个电阻的阻值均为6欧,电压U恒为18伏,求
如图所示的电路中,三个电阻的阻值均为6欧,电压U恒为18伏,求