题目内容
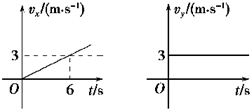 一快艇要从岸边某一不确定位置处到达河中离岸边100m远的一浮标处,已知快艇在静水中的速度vx图象和流水的速度vy图象如图所示,则( )
一快艇要从岸边某一不确定位置处到达河中离岸边100m远的一浮标处,已知快艇在静水中的速度vx图象和流水的速度vy图象如图所示,则( )| A、快艇的运动轨迹为直线 | B、快艇的运动轨迹为曲线 | C、能找到某一位置使快艇最快到达浮标处的时间为20 s | D、快艇最快到达浮标处经过的位移为100 m |
分析:将快艇的运动分解为沿河岸方向和垂直于河岸方向,两分运动一个做匀加速直线运动,一个做匀速直线运动,根据运动的合成确定其运动的轨迹.根据合运动与分运动具有等时性,在垂直于河岸方向上的速度越大,时间越短.即静水速垂直于河岸时,时间最短.根据平行四边形定则求出合位移.
解答:解:A、两分运动一个做匀加速直线运动,一个做匀速直线运动,知合加速度的方向与合速度的方向不在同一条直线上,合运动为曲线运动.故A错误、B正确.
C、静水速度垂直于河岸时,时间最短.在垂直于河岸方向上的加速度a=
=0.5m/s2,由d=
at2得,t=
=
s=20s,故C正确.
D、在沿河岸方向上的位移x=v2t=3×20m=60m,所以浮标处经过的位移s=
=20
m,故D错误.
故选:BC.
C、静水速度垂直于河岸时,时间最短.在垂直于河岸方向上的加速度a=
| 3 |
| 6 |
| 1 |
| 2 |
|
|
D、在沿河岸方向上的位移x=v2t=3×20m=60m,所以浮标处经过的位移s=
| x2+d2 |
| 34 |
故选:BC.
点评:解决本题的关键会将快艇的运动分解为沿河岸方向和垂直于河岸方向,知道在垂直于河岸方向上的速度越大,时间越短.以及知道分运动与合运动具有等时性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一快艇要从岸边某一不确定位置处到达河中离岸边100 m远的一浮标处,已知快艇在静水中的速度vx图象和流水的速度vy图象如图所示,则
| A.快艇的运动轨迹为直线 |
| B.快艇的运动轨迹为曲线 |
| C.能找到某一位置使快艇最快到达浮标处的时间为20 s |
| D.快艇最快到达浮标处经过的位移为100 m |
 一快艇要从岸边某一不确定位置处到达河中离岸边100m远的一浮标处,已知快艇在静水中的速度vx图象和水流的速度vy图象如图甲、乙所示,则下列说法中错误的是( )
一快艇要从岸边某一不确定位置处到达河中离岸边100m远的一浮标处,已知快艇在静水中的速度vx图象和水流的速度vy图象如图甲、乙所示,则下列说法中错误的是( )
