题目内容
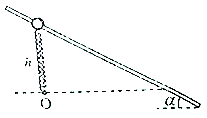
【题目】如图所示，在光滑水平桌面上有一光滑小孔O，一根轻绳穿过小孔，一端连接质量为m=1kg的小球A，另一端连接质量为M=4kg的重物B，已知g=10m/s2 ， 则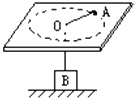
（1）当A球沿半径r=0.1m的圆周做匀速圆周运动，其角速度ω1为多大时，B物体处于将要离开、而尚未离开地面的临界状态？
（2）当小球A的角速度为ω2=10rad/s时，物体B对地面的压力为多大？
【答案】
（1）解：当B对地面恰好无压力时，有：Mg=FT′，
拉力 FT′提供小球A所需向心力，则：FT′=mrω′2
则有：ω′= 
答：角速度ω1为20rad/s时，B物体处于将要离开、而尚未离开地面的临界状态
（2）解：对小球A来说，小球受到的重力和支持力平衡．因此绳子的拉力提供向心力，则：
FT=mrω2=1×0.1×102N=10N，
对物体B来说，物体受到三个力的作用：重力Mg、绳子的拉力FT、地面的支持力FN，由力的平衡条件可得：
FT+FN=Mg 故 FN=Mg﹣FT
将FT=10N代入可得：FN=（4×10﹣10）N=30N
由牛顿第三定律可知，B对地面的压力为30 N，方向竖直向下
答：物体B对地面的压力为30N，方向竖直向下
【解析】（1）B物体处于将要离开而尚未离开地面的临界状态时地面给它的支持力为零，由此可以求出绳子上拉力，然后以A为研究对象根据向心力公式T=mω2r可以求出A球的角速度的大小．（2）对A，绳子的拉力提供A所需的向心力，根据向心力公式T=mω2r，求出绳子上拉力．B受到重力、支持力和拉力，根据B处于平衡状态，求出地面给B的支持力，根据牛顿第三定律可知物体B对地面的压力．
【考点精析】掌握向心力是解答本题的根本，需要知道向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力．
