题目内容
 (2009?湛江二模)(1)如图1所示,竖直放置的劲度系数为k的轻质弹簧,上端与质量为m、电荷量为+q的小球连接,小球与弹簧绝缘.下端与放在水平桌面上的质量也为m的物块相连.物块、弹簧和小球均处于静止状态.现突然加上一个竖直向上、电场强度为E的匀强电场,使某时刻物块对水平面的压力为零.求从加上匀强电场直到物块对水平面的压力为零的过程中,小球电势能改变量的大小.
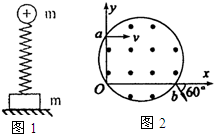
(2009?湛江二模)(1)如图1所示,竖直放置的劲度系数为k的轻质弹簧,上端与质量为m、电荷量为+q的小球连接,小球与弹簧绝缘.下端与放在水平桌面上的质量也为m的物块相连.物块、弹簧和小球均处于静止状态.现突然加上一个竖直向上、电场强度为E的匀强电场,使某时刻物块对水平面的压力为零.求从加上匀强电场直到物块对水平面的压力为零的过程中,小球电势能改变量的大小.(2)一个重力不计的带电粒子,电荷量为q,质量为m,从坐标(0,L)的a点平行于x轴射入磁感应强度为B的圆形匀强磁场区域又从x轴上b点射出磁场,速度方向与x轴正方向夹角为60°,如图2所示.试求:①带电粒子的速度大小;②粒子由a点运动到b点的时间.
分析:(1)由胡克定律可求得弹簧的压缩量,由功的公式可求得电场力所做的功;则由功能关系可求得小球电势能的改变量;
(2)带电粒子在电场中做匀速圆周运动;由几何关系可求得粒子的半径,再由洛仑兹力充当向心力可求得粒子运动的速度;由周期的表达式可求得粒子在磁场中运动的时间.
(2)带电粒子在电场中做匀速圆周运动;由几何关系可求得粒子的半径,再由洛仑兹力充当向心力可求得粒子运动的速度;由周期的表达式可求得粒子在磁场中运动的时间.
解答:解:(1)①设开始时弹簧压缩量为x1,由胡克定律有kx1=mg
当物块对地压力为零时弹簧伸长量为x2,此时有kx2=mg
此过程中电场力做功W=Eq(x1+x2)
联立以上各式可得:W=2
根据功能关系,电场力做正功等于电势能减少,因此电势能减少了
△Ep=W=
答:小球电势能改变量为
(2)设粒子在磁场中作圆周运动的半径为R,其运动的轨迹如答图3所示,由几何关系有:
=cos60°=
即R=2L
由牛顿第二定律有:
Bqv=m
由以上两式可得v=
②粒子在磁场中的运动的周期
T=
=
设粒子由a运动到b的时间为t,由几何关系可得ab弧所对的圆心角为θ=60°
t=
T=
答:①带电粒子的速度为
;②粒子从a到b运动的时间为
.
当物块对地压力为零时弹簧伸长量为x2,此时有kx2=mg
此过程中电场力做功W=Eq(x1+x2)
联立以上各式可得:W=2
| 2Eqmg |
| k |
根据功能关系,电场力做正功等于电势能减少,因此电势能减少了
△Ep=W=
| 2Eqmg |
| k |
答:小球电势能改变量为
| 2Eqmg |
| k |
(2)设粒子在磁场中作圆周运动的半径为R,其运动的轨迹如答图3所示,由几何关系有:
| R-L |
| R |
| 1 |
| 2 |
即R=2L
由牛顿第二定律有:
Bqv=m
| v2 |
| R |
由以上两式可得v=
| 2qBL |
| m |
②粒子在磁场中的运动的周期
T=
| 2πR |
| v |
| 2πm |
| Bq |
设粒子由a运动到b的时间为t,由几何关系可得ab弧所对的圆心角为θ=60°
t=
| θ |
| 360 |
| πm |
| 3Bq |
答:①带电粒子的速度为
| 2qBL |
| m |
| πm |
| 3Bq |
点评:(1)明确电场力所做的功等于电势能的改变量;
(2)带电粒子在磁场中的偏转类题目解决的方法是:定圆心、求半径,再由洛仑兹力充当向心力求出待求量.
(2)带电粒子在磁场中的偏转类题目解决的方法是:定圆心、求半径,再由洛仑兹力充当向心力求出待求量.

练习册系列答案
相关题目
 (2009?湛江二模)有一理想变压器的原线圈连接一只交流电流表,副线圈接入电路的匝数可以通过滑动触头Q调节,如图所示,在副线圈两输出端连接了定值电阻R0和滑动变阻器R,在原线圈上加一电压为U的交流电,则( )
(2009?湛江二模)有一理想变压器的原线圈连接一只交流电流表,副线圈接入电路的匝数可以通过滑动触头Q调节,如图所示,在副线圈两输出端连接了定值电阻R0和滑动变阻器R,在原线圈上加一电压为U的交流电,则( )