题目内容
20. 如图所示,物块质量m=3kg,以速度v=2m/s水平滑上一静止的平板车,平板车质量M=12kg,物块与平板车之间的动摩擦因数μ=0.2,其他摩擦不计(g取10m/s2),求:
如图所示,物块质量m=3kg,以速度v=2m/s水平滑上一静止的平板车,平板车质量M=12kg,物块与平板车之间的动摩擦因数μ=0.2,其他摩擦不计(g取10m/s2),求:(1)物块相对平板车静止时物块的速度;
(2)要使物块在平板车上不滑下,平板车至少多长.
分析 (1)物块与平板车组成的系统动量守恒,由动量守恒定律可以求出物块的速度.
(2)由动量定理可以求出物块的运动时间.由匀变速直线运动的平均速度公式求出物块与平板车的位移,然后求出平板车的最小长度.
解答 解:(1)物块与平板车组成的系统动量守恒,以物块与普遍车组成的系统为研究对象,以物块的速度方向为正方向,由动量守恒定律得:
mv=(M+m)v′,
代入数据解得:v′=0.4m/s;
(2)对物块由动量定理得:-μmgt=mv′-mv,
代入数据解得:t=0.8s;
物块在平板车上做匀减速直线运动,平板车做匀加速直线运动,由匀变速运动的平均速度公式,
对物块:s1=$\frac{v+v′}{2}$t,
对平板车:s2=$\frac{v′}{2}$t,
物块在平板车上滑行的距离:△s=s1-s2,
代入数据解得:△s=0.8s,
要使物块在平板车上不滑下,平板车至少长0.8m.
答:(1)物块相对平板车静止时物块的速度为0.4m/s;
(2)要使物块在平板车上不滑下,平板车至少长0.8m.
点评 本题考查了求出速度、运动时间与车的长度问题,分析清楚运动过程、应用动量守恒定律与动量定理、运动学公式即可正确解题.

练习册系列答案
相关题目
11.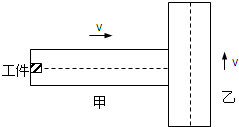 如图所示,某生产线上相互垂直的甲、乙传送带等高,宽度均为d,而且均以大小为v的速度运行,图中虚线为传送带中线.一个可以看做质点的工件从甲的左端释放,经过长时间后从甲的右端滑上乙,滑到乙的中线处恰好相对静止.下列说法正确的是( )
如图所示,某生产线上相互垂直的甲、乙传送带等高,宽度均为d,而且均以大小为v的速度运行,图中虚线为传送带中线.一个可以看做质点的工件从甲的左端释放,经过长时间后从甲的右端滑上乙,滑到乙的中线处恰好相对静止.下列说法正确的是( )
 如图所示,某生产线上相互垂直的甲、乙传送带等高,宽度均为d,而且均以大小为v的速度运行,图中虚线为传送带中线.一个可以看做质点的工件从甲的左端释放,经过长时间后从甲的右端滑上乙,滑到乙的中线处恰好相对静止.下列说法正确的是( )
如图所示,某生产线上相互垂直的甲、乙传送带等高,宽度均为d,而且均以大小为v的速度运行,图中虚线为传送带中线.一个可以看做质点的工件从甲的左端释放,经过长时间后从甲的右端滑上乙,滑到乙的中线处恰好相对静止.下列说法正确的是( )| A. | 工件在乙上运动痕迹为直线,长度为$\frac{{\sqrt{2}}}{2}d$ | |
| B. | 工件从滑到乙上到相对静止用时$\frac{d}{2v}$ | |
| C. | 工件与乙之间的动摩擦因数为$\frac{v^2}{gd}$ | |
| D. | 传送带乙对工件摩擦力做功为零 |
8.下列说法中正确的是( )
| A. | γ射线是原子受激发后向低能级跃迁时放出的 | |
| B. | 在稳定的重原子核中,质子数比中子数多 | |
| C. | 核反应过程中如果核子的平均质量减小,则要吸收核能 | |
| D. | 诊断甲状腺疾病时,注入的放射性同位素碘131作为示踪原子 |
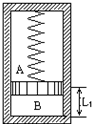 如图所示,可沿气缸壁自由活动的活塞将密封的圆筒形气缸分隔成A、B两部分.活塞与气缸顶部有一弹簧相连.当活塞位于气缸底部时弹簧恰好无形变.开始时B内充有一定量的气体,A内是真空.B部分高度为L1=0.1米、此时活塞受到的弹簧作用力与重力的大小相等.现将整个装置倒置,达到新的平衡后B部分的高度L2等于多少?(设气缸和外界导热良好,气体温度保持不变)
如图所示,可沿气缸壁自由活动的活塞将密封的圆筒形气缸分隔成A、B两部分.活塞与气缸顶部有一弹簧相连.当活塞位于气缸底部时弹簧恰好无形变.开始时B内充有一定量的气体,A内是真空.B部分高度为L1=0.1米、此时活塞受到的弹簧作用力与重力的大小相等.现将整个装置倒置,达到新的平衡后B部分的高度L2等于多少?(设气缸和外界导热良好,气体温度保持不变) 在“测定玻璃的折射率”实验中
在“测定玻璃的折射率”实验中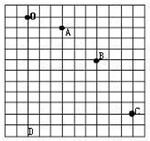 在“研究平抛物体的运动”实验中,在固定斜槽时,应该使斜槽末端水平,每次释放小球的位置应该相同.如图是小球做平抛运动时的一闪光照片,该照片记下平抛小球在运动中的几个位置O、A、B、C,其中O为小球刚作平抛运动时初位置,OD为竖直线,照片的闪光间隔是$\frac{1}{30}$s,小球的初速度为0.5m/s.(g=10m/s2,图中小方格均为正方形)
在“研究平抛物体的运动”实验中,在固定斜槽时,应该使斜槽末端水平,每次释放小球的位置应该相同.如图是小球做平抛运动时的一闪光照片,该照片记下平抛小球在运动中的几个位置O、A、B、C,其中O为小球刚作平抛运动时初位置,OD为竖直线,照片的闪光间隔是$\frac{1}{30}$s,小球的初速度为0.5m/s.(g=10m/s2,图中小方格均为正方形)