题目内容
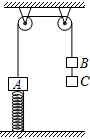 如图所示,一轻质弹簧下端固定在水平地面上,上端与物体A连接,物体A又与一跨过定滑轮的不可伸长的轻绳一端相连,绳另一端悬挂着物体B,B的下面又挂着物体C,A、B、C均处于静止状态.现剪断B和C之间的绳子,则A和B将做简谐运动.已知物体A质量为3m,B和C质量均为2m,A和B振动的振幅为d.试求:
如图所示,一轻质弹簧下端固定在水平地面上,上端与物体A连接,物体A又与一跨过定滑轮的不可伸长的轻绳一端相连,绳另一端悬挂着物体B,B的下面又挂着物体C,A、B、C均处于静止状态.现剪断B和C之间的绳子,则A和B将做简谐运动.已知物体A质量为3m,B和C质量均为2m,A和B振动的振幅为d.试求:
(1)物体A振动的最大速度;
(2)振动过程中,绳对物体B的最大拉力和最小拉力.
解:(1)绳剪断前,弹簧伸长量为x1,剪断后,在振动的平衡位置,弹簧压缩x2,
kx1=mg,kx2=mg,
由于x1=x2,两个状态的弹性势能相等(振动的振幅d=x1+x2);
由机械能守恒定律,有: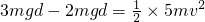 ,解得v=
,解得v=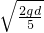 .
.
(2)B振动到最低点时拉力最大,为F1;振动到最高点时拉力最小,为F2;
B在振动过程的最低点:F1-2mg=2ma,3mg+kx1-F1=3ma,
解得:F1=2.8mg,
B在振动过程的最高点:2mg-F2=2ma,解得:F2=1.2mg.
答:(1)物体A振动的最大速度为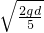 .
.
(2)振动过程中,绳对物体B的最大拉力和最小拉力分别为2.8mg、1.2mg.
分析:(1)根据胡克定律,通过共点力平衡分别求出绳子剪断前弹簧的伸长量以及绳子剪断后,弹簧在平衡位置时的压缩量.发现两个位置伸长量和压缩量相等,则弹簧势能相等,结合机械能守恒定律求出在平衡位置时的速度,即最大速度.
(2)B振动到最低点时拉力最大,振动到最高点时拉力最小,根据牛顿第二定律求出最大拉力和最小拉力.
点评:本题综合考查了胡克定律、机械能守恒定律和牛顿第二定律,综合性较强,对学生的能力要求较高,需加强训练.
kx1=mg,kx2=mg,
由于x1=x2,两个状态的弹性势能相等(振动的振幅d=x1+x2);
由机械能守恒定律,有:
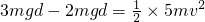 ,解得v=
,解得v=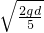 .
.(2)B振动到最低点时拉力最大,为F1;振动到最高点时拉力最小,为F2;
B在振动过程的最低点:F1-2mg=2ma,3mg+kx1-F1=3ma,
解得:F1=2.8mg,
B在振动过程的最高点:2mg-F2=2ma,解得:F2=1.2mg.
答:(1)物体A振动的最大速度为
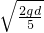 .
.(2)振动过程中,绳对物体B的最大拉力和最小拉力分别为2.8mg、1.2mg.
分析:(1)根据胡克定律,通过共点力平衡分别求出绳子剪断前弹簧的伸长量以及绳子剪断后,弹簧在平衡位置时的压缩量.发现两个位置伸长量和压缩量相等,则弹簧势能相等,结合机械能守恒定律求出在平衡位置时的速度,即最大速度.
(2)B振动到最低点时拉力最大,振动到最高点时拉力最小,根据牛顿第二定律求出最大拉力和最小拉力.
点评:本题综合考查了胡克定律、机械能守恒定律和牛顿第二定律,综合性较强,对学生的能力要求较高,需加强训练.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( )
如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( ) 如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( )
如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( ) 如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )
如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )