题目内容
摩托车的最大行驶速度为vm=30m/s,为使其从静止开始做匀加速直线运动而在t=100s内追上前方s=975m处以v=18m/s的速度匀速行驶的卡车,摩托车至少要以多大的加速度a行驶?
【答案】分析:根据摩托车的位移等于卡车位移和s之和,求出运动的加速度,判断摩托车的速度有无超过最大速度,若摩托车的末速度大于最大速度,则摩托车在追赶的过程中先做匀加速直线运动,再做匀速直线运动,然后根据位移关系,求出摩托车的加速度.
解答:解:先判断:若设
 at2=vt+s.
at2=vt+s.
代入t=100s,v=18m/s,s=975m
后可求得 a=0.555m/s2
则100s末摩托车的速度为
at=55.5m/s>30m/s 显然不正确
由于受到最大行驶速度30m/s的制约,摩托车的实际运动过程是:
先做初速为零的匀加速直线运动,当速度达到最大值后又继续做匀速直线运动.
由运动规律列出方程
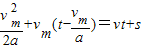
将相关数据vm=30m/s,t=100s,v=18m/s,s=975m代入,
便可得a=2m/s2.
故摩托车至少要以2m/s2的加速度行驶.
点评:解决本题关键要先搞清摩托车在追赶卡车的过程中做什么运动,然后根据摩托车和卡车的位移关系求出摩托车的最小加速度.
解答:解:先判断:若设
 at2=vt+s.
at2=vt+s.代入t=100s,v=18m/s,s=975m
后可求得 a=0.555m/s2
则100s末摩托车的速度为
at=55.5m/s>30m/s 显然不正确
由于受到最大行驶速度30m/s的制约,摩托车的实际运动过程是:
先做初速为零的匀加速直线运动,当速度达到最大值后又继续做匀速直线运动.
由运动规律列出方程
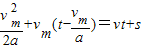
将相关数据vm=30m/s,t=100s,v=18m/s,s=975m代入,
便可得a=2m/s2.
故摩托车至少要以2m/s2的加速度行驶.
点评:解决本题关键要先搞清摩托车在追赶卡车的过程中做什么运动,然后根据摩托车和卡车的位移关系求出摩托车的最小加速度.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目