题目内容
【题目】用密度为d、电阻率为ρ、粗细均匀的金属导线制成两个闭合正方形线框M和N，边长均为L，线框M、N的导线横截面积分别为S1、S2，且S1＞S2，如图所示．匀强磁场仅存在于相对磁极之间，磁感应强度大小为B，其他地方的磁场忽略不计．金属线框M水平放在磁场上边界的狭缝间，线框平面与磁场方向平行，开始运动时可认为M的aa′边和bb′边都处在磁场中．线框N在线框M的正上方，与线框M相距为h．两线框均从静止开始同时释放，其平面在下落过程中保持水平．设磁场区域在竖直方向足够长，不计空气阻力及两线框间的相互作用．
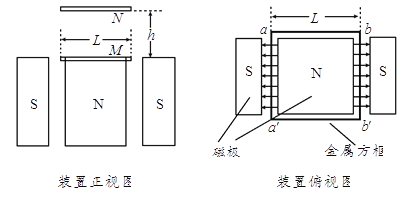
(1)计算线框N刚进入磁场时产生的感应电流；
(2)在下落过程中，若线框N恰能追上线框M，N追上M时，M下落的高度为H，N追上M之前N一直做减速运动，求该过程中线框N产生的焦耳热；
(3)若将线框M、N均由磁场上边界处先后释放，释放的时间间隔为t，计算两线框在运动过程中的最大距离．
【答案】(1) 
(2) 
(3) Δx＝
【解析】(1)线框N进入磁场前，有 
刚进入磁场时，有 E＝2BLv1
线框N中的感应电流 
其中 
联立解得
(2)当线框M在磁场中运动达到匀速时，设速度为v2，有G＝F安
其中线框重力G＝mg＝4LS1dg
安培力F安＝2BIL＝
解得
由上式可知匀速运动速度与导线截面积无关，所以两线框匀速运动速度相同，均为v2．由此可知当线框N恰好追上M时，两者速度相等．选N为研究对象，根据能量守恒可得N产生的焦耳热
(3)线框释放后二者先后作变速运动
mg－F＝ma
即4LSdg－
＝4LSda
解得a＝g－
由加速度可知：线框下落的加速度与线框的导线截面积无关，两个线框在磁场中先后作相同的加速运动，当a减小到0时做匀速运动，所以只要后释放的线框还未达到匀速时，先释放线的框速度就比较大，二者的距离就会继续增大，当二者都做匀速运动时，间距最大．
此时最大间距Δx＝v2t＝
