题目内容
物体A从距离地面某高度处由静止开始下落，落地时速度刚好等于地球的第一宇宙速度．已知地球半径为R，以无穷远为零势能面，物体在距地球球心为r（r≥R）的位置处重力势能为Ep=-
（其中M为地球质量，m为物体的质量），不计物体运动中所受的阻力，则物体A从距地面多高处下落？（ ）
| GMm |
| r |
| A、R | B、2R | C、3R | D、4R |
分析：物体A从距离地面某高度处由静止开始下落，不计物体运动中所受的阻力，下落过程机械能守恒．重力势能减小，动能增加．达到第一宇宙速度时，牛顿第二定律可得此时的动能，进而可得到此时的机械能的总量，进而可得物体刚刚下落时的机械能的总量，也就是下落时的重力势能，据此可解物体下落时的高度．
解答：解：设第一宇宙速度为v，由牛顿第二定律可得：
=
故有：Ek=
mv2=
W物体在地球表面的重力势能为：Ep=-
故此时物体的机械能总量为：E=Ek+EP=-
所以，设物体下落高度为h，则有：-
=-
故有：h=R．
故选：A．
| GMm |
| R2 |
| mv2 |
| R |
故有：Ek=
| 1 |
| 2 |
| GMm |
| 2R |
W物体在地球表面的重力势能为：Ep=-
| GMm |
| R |
故此时物体的机械能总量为：E=Ek+EP=-
| GMm |
| 2R |
所以，设物体下落高度为h，则有：-
| GMm |
| (R+h) |
| GMm |
| 2R |
故有：h=R．
故选：A．
点评：关键知道下落过程机械能守恒，结合第一宇宙速度的动力学方程得到动能表达式，利用重力势能的表达式联合求解，难度不大．
练习册系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
如图所示，物体甲从高H处以速度v1平抛，同时物体乙从距甲水平方向距离x处由地面以速度v2竖直上抛，不计空气阻力，两个物体在空中某处相遇，下列叙述中正确的是（ ）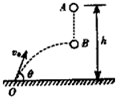
如图所示，从地面上某处O以初速度射出一个颗子弹，同时从距地面高为h处的A点自由落下一物体，若两者在B点相遇，B点离O点的水平距离为L，求子弹的初速度与水平方向的夹角θ？
V/m竖直向上的匀强电场，有一质量m=lkg带电量q=1.4×
C正电荷的物体（可视为质点），从A点的正上方距离A点H处由静止开始自由下落（不计空气阻力），BC段为长L=2m，与物体动摩擦因素
=0.2的粗糙绝缘水平面，CD段为倾角
=
且离地面DE高h=0.8m的斜面。求：
，请通过计算标示出物体从C处射出后打到的范围。（已知
。不需要计算过程，但要具体的位置。不讨论物体的反弹以后的情况。）
