题目内容
如图所示，内截面积为S=10-4m2、足够高的圆柱形气缸开口向上竖直放置在水平面上，缸内离底部高为h1=0.08m处有一质量为m=0.2kg的活塞封住一定质量的理想气体，气体温度为t1=27°C，大气压强为p0=1.0×105Pa，重力加速度为g=10m/s2．问：（1）若把活塞用销子固定住，再将气体温度升高到t2=102℃，此时缸内气体的压强p2为多大？
（2）若在初始条件下，保持气体温度不变，把气缸倒过来，开口向下竖直放置，此时活塞与气缸底的距离h2为多大？
分析：（1）若把活塞用销子固定住，则封闭气体做等容变化，找出初末状态参量，根据查理定律列式求解即可；
（2）保持气体温度不变，则封闭气体做等温变化，找出初末状态参量，根据玻意耳定律列式求解即可
（2）保持气体温度不变，则封闭气体做等温变化，找出初末状态参量，根据玻意耳定律列式求解即可
解答：解；（1）初态：P1=P0+
=1.2×105Pa T1=300K T2=375K
封闭气体做等容变化，根据查理定律得：
=
代入数据求得：p2=1.5×105Pa
（2）P3=P0-
=0.8×105Pa
封闭气体做等温变化，根据玻意耳定律得：p1h1S=p3h2S
代入数据求得：h2=12cm
答：（1）缸内气体的压强p2为1.5×105Pa
（2）活塞与气缸底的距离h2为12cm．
| mg |
| s |
封闭气体做等容变化，根据查理定律得：
| P1 |
| T1 |
| P2 |
| T2 |
代入数据求得：p2=1.5×105Pa
（2）P3=P0-
| mg |
| s |
封闭气体做等温变化，根据玻意耳定律得：p1h1S=p3h2S
代入数据求得：h2=12cm
答：（1）缸内气体的压强p2为1.5×105Pa
（2）活塞与气缸底的距离h2为12cm．
点评：本题关键根据平衡条件得到封闭气体的压强，然后得到封闭气体初末状态的各个状态参量，根据气体实验定律列式求解即可
练习册系列答案
活力课时同步练习册系列答案
相关题目
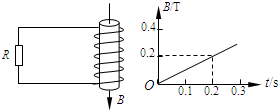如图所示，横截面积为S=0.10m2，匝数为N=120匝的闭合线圈放在平行于线圈轴线的匀强磁场中，该匀强磁场的磁感应强度B随时间t变化的规律如图所示．线圈电阻为r=1.2Ω，电阻R=4.8Ω．求：
如图所示，横截面积为S=0.20m2，匝数为N=100匝的闭合线圈放在平行于线圈轴线的匀强磁场中，该匀强磁场的磁感应强度B随时间t变化的规律如图所示．线圈电阻为r=1.2Ω，电阻R=4.8Ω．求：
