题目内容
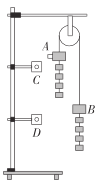
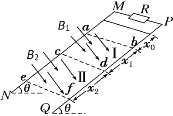
【题目】如图所示,两平行且无限长光滑金属导轨MN、PQ与水平面的夹角为θ=37°,两导轨之间相距为L=1m,两导轨M、P间接入电阻R=1Ω,导轨电阻不计。在abdc区域内有一个方向垂直于两导轨平面向下的匀强磁场Ⅰ,磁感应强度为B1=2T,磁场的宽度x1=3m,在cd连线以下的区域有一个方向也垂直于两导轨平面向下的匀强磁场Ⅱ,磁感应强度为B2=1T。一个质量为m=1kg的金属棒垂直放在金属导轨上,与导轨接触良好,金属棒的电阻r=1Ω。若将金属棒在离ab连线上端x0处自由释放,则金属棒进入磁场Ⅰ恰好做匀速直线运动。金属棒进入磁场Ⅱ后,经过ef时刚好达到平衡状态,cd与ef之间的距离x2=9m。重力加速度g取10m/s2,sin37=0.6,求金属棒:
(1)在磁场Ⅰ区域内速度v1的大小;
(2)从开始运动到在磁场Ⅱ中达到平衡状态这一过程中整个电路产生的热量;
(3)从开始运动到在磁场Ⅱ中达到平衡状态所经过的时间。
【答案】(1)3m/s;(2)4.5J;(3)3.75s
【解析】
(1)金属棒进入磁场Ⅰ区域匀速运动,由平衡条件和电磁感应规律得
I=![]()
mgsin37°=B1IL
![]()
解得
v1=3m/s
(2)金属棒在未进入磁场前做初速度为零的匀加速直线运动,知
mgsin37°=ma
得
a=6m/s2
2ax0=v12
得
x0=0.75m
金属棒在通过磁场Ⅱ区域达到稳定状态时,重力沿斜轨道向下的分力与安培力相等
I′=![]()
mgsin37°=B2I′L
![]()
解得
v2=12m/s
金属棒从开始运动到在磁场Ⅱ区域中达到稳定状态过程中,根据动能定理,有
mg(x0+x1+x2)sin37°+W安=![]() mv22-0
mv22-0
![]()
电路在此过程中产生的热量
Q=-W安=4.5J
(3)由运动学规律得
先匀加速
v1=at1
t1=0.5s
之后匀速
x1=v1t2
t2=1s
最后,金属棒在磁场Ⅱ中达到稳定状态前的过程中取任意微小过程,设这一微小过程的时间为Δti,速度为vi,速度的变化量为Δvi,金属棒从进入磁场Ⅱ到在磁场Ⅱ中达到稳定状态的过程中,有
mgsin37°∑Δti-![]() =m∑Δvi
=m∑Δvi
mgsin37°t3-![]() =m(v2-v1)
=m(v2-v1)
解得
t3=2.25s
所以
t=t1+t2+t3=0.5+1+2.25s=3.75s