Question

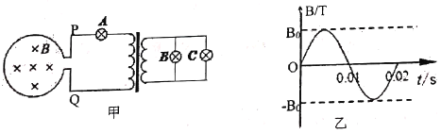
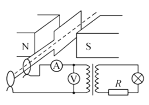
【题目】如图甲所示为足够长、倾斜放置的平行光滑导轨，处在垂直斜面向上的匀强磁场中，导轨上端接 有一定值电阻，导轨平面的倾角为 37°，金属棒垂直导轨放置，用一平行于斜面向上的拉力 F 拉着金属棒由静止向上运动，金属棒的质量为 0.2kg，其速度大小随加速度大小的变化关系如图乙所示，且金属棒由静止加速到最大速度的时间为 1s，金属棒和导轨的电阻不计，sin 37°=0.6，cos 37°=0.8，g取 10m/s2，则（　　）

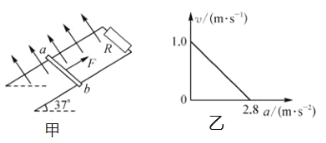
A.F的大小会随着棒高度的变化而变化

B.回路中的最大电功率等于 0.56W

C.F的最大功率为 0.56W

D.金属棒由静止加速到最大速度这段时间内定值电阻上产生的焦耳热是 0.26J

Answer 1

【答案】BD

【解析】

A． 金属棒速度为v时，受到的安培力大小为：

根据牛顿第二定律得：

得：

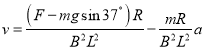
根据数学知识可知：

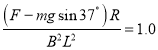
因m、B、L、R都是定值，所以F为恒力，故A错误；

BC． 金属棒做加速度逐渐减小的变加速运动，当加速度为零时速度最大，F的功率最大，设ab棒受到的最大安培力大小为FAm，则有：

v=0时，有：

由图知v=0时，a0=2.8m/s2，联立解得

F=1.76N，FAm=0.56N

F的最大功率为：

PF=Fvm=1.76×1W=1.76W

回路中的最大电功率为：

P电=FAmvm=0.56×1W=0.56W

故B正确，C错误；

D． 设金属棒由静止加速到最大速度这段时间内通过的位移为x。根据动量定理得：

又

根据能量守恒得：

结合

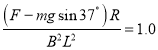
定值电阻上产生的焦耳热

Q=0.26J

故D正确。

故选BD。