题目内容
（注意：在试卷题上作答无效）
如右图，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动，星球A和B两者中心之间的距离为L。已知A、B的中心和O三点始终共线，A和B分别在O的两侧。引力常数为G。
（1）求两星球做圆周运动的周期：
（2）在地月系统中，若忽略其他星球的影响，可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行的周期为T1。但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期记为T2。已知地球和月球的质量分别为5.98×1024kg和7.35×1022kg。求T2与T1两者平方之比。（结果保留3位小数）
⑴
⑵1.01
解析: ⑴A和B绕O做匀速圆周运动，它们之间的万有引力提供向心力，则A和B的向心力相等。且A和B和O始终共线，说明A和B有相同的角速度和周期。
则有：
，
，解得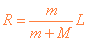
，
对A根据牛顿第二定律和万有引力定律得
化简得
⑵将地月看成双星，由⑴得
将月球看作绕地心做圆周运动，根据牛顿第二定律和万有引力定律得
化简得 
所以两种周期的平方比值为
练习册系列答案
相关题目
如图，在
区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B。在t=0 时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向夹角分布在0~180°范围内。已知沿y轴正方向发射的粒子在t=
时刻刚好从磁场边界上P(
,a)点离开磁场。求：
如图，在
区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B。在t=0 时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向夹角分布在0~180°范围内。已知沿y轴正方向发射的粒子在t=
时刻刚好从磁场边界上P(
,a)点离开磁场。求：
（注意：在试卷题上作答无效）