题目内容
 (2006?深圳二模)有一个竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一个质量为m的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA轨道回到点A,到达A点时对轨道的压力为4mg.
(2006?深圳二模)有一个竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一个质量为m的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA轨道回到点A,到达A点时对轨道的压力为4mg.在求小球在A点的速度V0时,甲同学的解法是:由于小球恰好到达B点,故在B点小球的速度为零,
| 1 |
| 2 |
| v | 2 0 |
| gR |
在求小球由BFA回到A点的速度时,乙同学的解法是:由于回到A点时对轨道的压力为4mg
故:4mg=m
| ||
| R |
| gR |
你同意甲、乙两位同学的解法吗?如果同意请说明理由;若不同意,请指出他们的错误之处,并求出结果.根据题中所描绘的物理过程,求小球由B经F回到A的过程中克服摩擦力所做的功.
分析:可根据牛顿第二定律列出重力提供向心力,与动能定理相结合,即可求出初速度.对研究对象进行受力分析,从而确定提供向心力的来源.最后由动能定理来确定克服摩擦力做功的值.
解答:解:
不同意;
甲同学在求V0时,认为小球在B点的速度为零,这是错误的,在B点VB有最小值.
正确的解法是:mg=m
①
-2mgR=
m
-
m
②
联立①、②求解得:v0=
乙同学在计算中漏掉了重力,应为:FN-mg=m
③
将FN=4mg代入解得:vA=
设摩擦力做得功为Wf,小球从B→F→A的过程中由动能定理可得:2mgR+Wf=
m
-
m
④
解得:Wf=-mgR
故小球从B→F→A的过程中克服摩擦力做得功为Wf=mgR.
答:小球由B经F回到A的过程中克服摩擦力所做的功mgR.
不同意;
甲同学在求V0时,认为小球在B点的速度为零,这是错误的,在B点VB有最小值.
正确的解法是:mg=m
| ||
| R |
-2mgR=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 0 |
联立①、②求解得:v0=
| 5gR |
乙同学在计算中漏掉了重力,应为:FN-mg=m
| ||
| R |
将FN=4mg代入解得:vA=
| 3gR |
设摩擦力做得功为Wf,小球从B→F→A的过程中由动能定理可得:2mgR+Wf=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
解得:Wf=-mgR
故小球从B→F→A的过程中克服摩擦力做得功为Wf=mgR.
答:小球由B经F回到A的过程中克服摩擦力所做的功mgR.
点评:考查动能定理与牛顿第二定律的应用,掌握提供向心力的来源的方法.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 (2006?深圳二模)如图所示,一束截面为圆形(半径R)的平行白光垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形彩色亮区.已知玻璃半球的半径为R,屏幕S至球心的距离为D(D>4R),不考虑光的干涉和衍射,试问:
(2006?深圳二模)如图所示,一束截面为圆形(半径R)的平行白光垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形彩色亮区.已知玻璃半球的半径为R,屏幕S至球心的距离为D(D>4R),不考虑光的干涉和衍射,试问: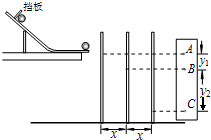 (2006?深圳二模)在做“研究平抛物体的运动”的实验时,为了确定小球在不同时刻所通过的位置,用如图所示的装置:将一块平木板钉上复写纸和白纸,竖直立于槽口前某处且和斜槽所在的平面垂直,使小球从斜槽上紧靠挡板处由静止滚下,小球撞在木板上留下痕迹A;将木板向后移距离x,再使小球从斜槽上紧靠挡板处由静止滚下,小球撞在木板上留下痕迹B;又将木板再向后移距离x,小球再从斜槽上紧靠挡板处由静止滚下,再得到痕迹C.若测得木板每次后移距离x=20.0cm,A、B间距离y1=5.0cm,B、C间距离y2=15.0cm.(g取10.0m/s2) 根据以上直接测量的物理量推导出小球初速度的计算公式为v0=
(2006?深圳二模)在做“研究平抛物体的运动”的实验时,为了确定小球在不同时刻所通过的位置,用如图所示的装置:将一块平木板钉上复写纸和白纸,竖直立于槽口前某处且和斜槽所在的平面垂直,使小球从斜槽上紧靠挡板处由静止滚下,小球撞在木板上留下痕迹A;将木板向后移距离x,再使小球从斜槽上紧靠挡板处由静止滚下,小球撞在木板上留下痕迹B;又将木板再向后移距离x,小球再从斜槽上紧靠挡板处由静止滚下,再得到痕迹C.若测得木板每次后移距离x=20.0cm,A、B间距离y1=5.0cm,B、C间距离y2=15.0cm.(g取10.0m/s2) 根据以上直接测量的物理量推导出小球初速度的计算公式为v0=