题目内容
5.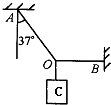 如图,轻绳OA一端系在天花板上,与竖直线夹角37°,轻绳OB水平,一端系在墙上,O点处挂一重为80N的物体.(cos37°=0.8,sin37°=0.6)
如图,轻绳OA一端系在天花板上,与竖直线夹角37°,轻绳OB水平,一端系在墙上,O点处挂一重为80N的物体.(cos37°=0.8,sin37°=0.6)(1)求AO、BO的拉力各为多大?
(2)若AO、BO、CO所能承受的最大拉力均为200N,则所吊重物重力最大不能超过多大?
分析 (1)对结点O受力分析,通过共点力平衡求出AO、BO绳的拉力.
(2)根据受力判断哪根绳承受的拉力先达到最大,再结合共点力平衡条件求出重物的重力最大值.
解答 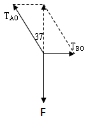 解:(1)对结点O受力分析,如图所示:
解:(1)对结点O受力分析,如图所示:
根据共点力平衡条件,有:F=G=80N
TAO=$\frac{F}{cos37°}$=$\frac{80}{0.8}$N=100N
TBO=Ftan37°=80×$\frac{3}{4}$N=60N
(2)O点受三个力作用而处于平衡状态,结合图中三角形知识,可知由于TOA>TOC>TOB,所以随着重物的重力增大,AO绳的拉力最先达到最大值,当 TAO=200N时,Fmax=TOAcos37°=200×0.8N=160N
答:(1)OA、OB的拉力分别为100N、60N.
(2)所吊重物重力最大不能超过160N.
点评 本题是物体平衡中临界问题,其关键是分析物体受力、正确作出力的合成图.

练习册系列答案
相关题目
15.以8m/s匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线18m.该车加速时最大加速度大小为2m/s2,减速时最大加速度大小为6m/s2.此路段允许行驶的最大速度为12.5m/s,下列说法中正确的有( )
| A. | 如果立即做匀加速运动,在绿灯熄灭前汽车一定通过停车线 | |
| B. | 如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速 | |
| C. | 如果距停车线5m处减速,汽车能停在停车线处 | |
| D. | 如果立即做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线 |
16.在平直公路上,自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们的位移s(m)随时间t(s)变化的规律为:汽车s=10t-$\frac{1}{4}$t2为,自行车为s=6t,则下列说法正确的是( )
| A. | 汽车作匀减速直线运动,自行车作匀速运动 | |
| B. | 不能确定汽车和自行车各作什么运动 | |
| C. | 开始经过路标后较小时间内汽车在前,自行车在后 | |
| D. | 甲车的加速度大小为0.5m/s2 |
10.下面描述的几个速度中,属于瞬时速度的是( )
| A. | 子弹以790/s的速度击中目标 | |
| B. | 信号沿动物神经传播的速度大约为10m/s | |
| C. | 汽车上速度计的示数为80km/h | |
| D. | 台风以360m/s的速度向东北方向移动 |
17.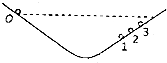 伽利略创造的把实验、假设和逻辑锥理相结合的科学方法,有力地促进了人类科学认设的发展,利用如图所示的装置做如下实验;小球从左侧斜面上的O点由静止释放后沿斜面向下运动,并沿右侧斜面上升.斜面上先后铺垫三种粗糙程度逐渐降低的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3,根据三次实验结果的对比,可以得到的最直接的结论是( )
伽利略创造的把实验、假设和逻辑锥理相结合的科学方法,有力地促进了人类科学认设的发展,利用如图所示的装置做如下实验;小球从左侧斜面上的O点由静止释放后沿斜面向下运动,并沿右侧斜面上升.斜面上先后铺垫三种粗糙程度逐渐降低的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3,根据三次实验结果的对比,可以得到的最直接的结论是( )
 伽利略创造的把实验、假设和逻辑锥理相结合的科学方法,有力地促进了人类科学认设的发展,利用如图所示的装置做如下实验;小球从左侧斜面上的O点由静止释放后沿斜面向下运动,并沿右侧斜面上升.斜面上先后铺垫三种粗糙程度逐渐降低的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3,根据三次实验结果的对比,可以得到的最直接的结论是( )
伽利略创造的把实验、假设和逻辑锥理相结合的科学方法,有力地促进了人类科学认设的发展,利用如图所示的装置做如下实验;小球从左侧斜面上的O点由静止释放后沿斜面向下运动,并沿右侧斜面上升.斜面上先后铺垫三种粗糙程度逐渐降低的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3,根据三次实验结果的对比,可以得到的最直接的结论是( )| A. | 如果小球受力的作用,它的运动状态将发生改变 | |
| B. | 如果小球不受力,它将一直保持匀速运动或静止状态 | |
| C. | 如果斜面光滑,小球将上升到与O点等高的位置 | |
| D. | 小球受到的力一定时,质量越大,它的加速度越小 |
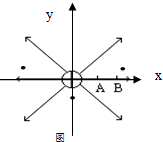 如图所示,是一正点电荷电场的电场线,电场中A、B两点间的电势差UAB=200V.电量为+6×10-8C的电荷从A移到B,电场力对其做的功为1.2×10-5J,其电势能减小.(填增大、减小或不变),EA>EB(填>,=或<)
如图所示,是一正点电荷电场的电场线,电场中A、B两点间的电势差UAB=200V.电量为+6×10-8C的电荷从A移到B,电场力对其做的功为1.2×10-5J,其电势能减小.(填增大、减小或不变),EA>EB(填>,=或<)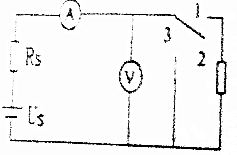 如图所示电路,已知US=10V,RS=2Ω,R=18Ω,求开关S分别打在1、2、3位置时,电压表和电流表的读数.
如图所示电路,已知US=10V,RS=2Ω,R=18Ω,求开关S分别打在1、2、3位置时,电压表和电流表的读数.