题目内容
天花板下悬挂着两个固定的光滑裸露导线圆环半径为r=0.5m，相距L=1m，然后连接电路，电源电动势E=3V，并且放入一个竖直向上的匀强磁场，B=0.4T．现在将一根质量m=60g，B电阻R=1.5Ω的金属棒搁置其上．闭合开关后，金属棒会上滑一定距离最后静止在圆环某位置．问此金属棒上升高度H=？此过程安培力做功W=？（不计其它电阻，重力加速度g=10m/s2）
【答案】分析：金属棒最后静止在圆环某位置，对金属棒进行受力分析，根据平衡条件和几何关系求解上升的高度．
根据动能定理研究金属棒上滑一定距离最后静止的过程求解安培力做功．
解答：解：（1）对棒进行受力分析：
因为静止根据平衡条件得：
tanα=
=
而I=
得tanα=
所以金属棒上升的高度H=（R-Rcosα）=0.2m
（2）根据动能定理研究金属棒上滑一定距离最后静止的过程得：
W安-mgH=0-0=0
得W安=0.12J
答：此金属棒上升高度是0.2m，此过程安培力做功是0.12J．
点评：要通过受力分析和平衡条件得出最后静止位置的几何关系．
动能定理是求解变力做功的常用方法．
根据动能定理研究金属棒上滑一定距离最后静止的过程求解安培力做功．
解答：解：（1）对棒进行受力分析：
因为静止根据平衡条件得：
tanα=
=而I=
得tanα=
所以金属棒上升的高度H=（R-Rcosα）=0.2m
（2）根据动能定理研究金属棒上滑一定距离最后静止的过程得：
W安-mgH=0-0=0
得W安=0.12J
答：此金属棒上升高度是0.2m，此过程安培力做功是0.12J．
点评：要通过受力分析和平衡条件得出最后静止位置的几何关系．
动能定理是求解变力做功的常用方法．
练习册系列答案
名校课堂系列答案
相关题目
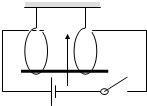天花板下悬挂着两个固定的光滑裸露导线圆环半径为r=0.5m，相距L=1m，然后连接电路，电源电动势E=3V，并且放入一个竖直向上的匀强磁场，B=0.4T．现在将一根质量m=60g，B电阻R=1.5Ω的金属棒搁置其上．闭合开关后，金属棒会上滑一定距离最后静止在圆环某位置．问此金属棒上升高度H=？此过程安培力做功W=？（不计其它电阻，重力加速度g=10m/s2）
