题目内容
1.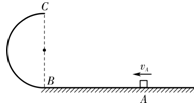 如图所示,竖直平面内的半圆形轨道下端与水平面相切,B、C分别为半圆形轨道的最低点和最高点.小滑块(可视为质点)沿水平面向左滑动,经过A点时的速度vA,恰好通过最高点C.已知半圆形轨道光滑,半径R=0.40m,滑块与水平面间的动摩擦因数μ=0.50,A、B两点间的距离L=1.30m.取重力加速度g=10m/s2.求:
如图所示,竖直平面内的半圆形轨道下端与水平面相切,B、C分别为半圆形轨道的最低点和最高点.小滑块(可视为质点)沿水平面向左滑动,经过A点时的速度vA,恰好通过最高点C.已知半圆形轨道光滑,半径R=0.40m,滑块与水平面间的动摩擦因数μ=0.50,A、B两点间的距离L=1.30m.取重力加速度g=10m/s2.求:(1)滑块运动到A点时速度的大小vA
(2)滑块从C点水平飞出后,落地点与B点间的距离x.
分析 (1)由向心力公式可求得C点的动能,再由动能定理可求得A点的速度;
(2)小滑块飞出后做平抛运动,由运动的合成与分解可求得水平位移.
解答 解:(1)小球恰好通过C点,有:mg=m$\frac{{v}_{C}^{2}}{R}$
代入数据解得:vc=2m/s;
由A 到 C过程,由动能定理得:-μmgL-mg×2R=$\frac{1}{2}$mvc2-$\frac{1}{2}$mvA2
代入数据得:vA=$\sqrt{33}$m/s;
(2)小滑块从C飞出后,做平抛运动
水平方向x=vct
竖直方向2R=$\frac{1}{2}$gt2;
解得:x=0.8m
答:(1)滑块运动到A点时速度的大小vA为$\sqrt{33}$m/s;
(2)滑块从C点水平飞出后,落地点与B点间的距离x为0.8m
点评 本题考查向心力公式、动能定理及平抛运动的规律,在解题时要特别注意竖直方向圆周运动临界值的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 测定运动员体能的一种装置如图所示,运动员质量为m1,绳拴在腰间沿水平方向跨过一个轻质且不计摩擦的滑轮,悬挂重物m2,人用力蹬传送带而人的重心相对于地面不动,使传送带上侧以速率v向右运动,下面是关于人对传送带做功的说法,正确的是( )
测定运动员体能的一种装置如图所示,运动员质量为m1,绳拴在腰间沿水平方向跨过一个轻质且不计摩擦的滑轮,悬挂重物m2,人用力蹬传送带而人的重心相对于地面不动,使传送带上侧以速率v向右运动,下面是关于人对传送带做功的说法,正确的是( )
 测定运动员体能的一种装置如图所示,运动员质量为m1,绳拴在腰间沿水平方向跨过一个轻质且不计摩擦的滑轮,悬挂重物m2,人用力蹬传送带而人的重心相对于地面不动,使传送带上侧以速率v向右运动,下面是关于人对传送带做功的说法,正确的是( )
测定运动员体能的一种装置如图所示,运动员质量为m1,绳拴在腰间沿水平方向跨过一个轻质且不计摩擦的滑轮,悬挂重物m2,人用力蹬传送带而人的重心相对于地面不动,使传送带上侧以速率v向右运动,下面是关于人对传送带做功的说法,正确的是( )| A. | 人对传送带做负功 | B. | 人对传送带不做功 | ||
| C. | 人对传送带做功的功率为m2gv | D. | 人对传送带做功的 功率为(m1+m2)gv |
10.一列简谐横波沿x轴正方向传播,P点振动周期为0.5s,在某一时刻波形如图所示,可判断( ) 

| A. | P点此时刻振动方向沿y轴负方向 | |
| B. | 该波波速为4m/s | |
| C. | 在离波源为11m的Q点开始振动时沿y轴负方向运动 | |
| D. | 当Q点达到波峰时,E点达到波谷 |
11. 如图,一束光沿半径方向射向一块半圆形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线,则( )
如图,一束光沿半径方向射向一块半圆形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线,则( )
 如图,一束光沿半径方向射向一块半圆形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线,则( )
如图,一束光沿半径方向射向一块半圆形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线,则( )| A. | 在玻璃中,a光的传播速度小于b光的传播速度 | |
| B. | 在真空中,a光的波长小于b光的波长 | |
| C. | 若改变光束的入射方向使θ角逐渐变大,则折射光线b首先消失 | |
| D. | 分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距 |
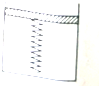 如图所示,一端封闭的薄壁金属筒,开口向上静止于水平面上,一横截面积为S=30cm2的轻质活塞放于金属筒内,封闭良好且无摩擦,一轻弹簧在筒内与活塞和筒底部同时接触,处于自然章台,已知弹簧劲度系数k=625N/m,原长L0=20cm,环境温度恒定,大气压P0=1.0×105Pa,现在活塞上方放一质量m=10kg的物块,重力加速度g=10m/s,求稳定后弹簧的压缩量.
如图所示,一端封闭的薄壁金属筒,开口向上静止于水平面上,一横截面积为S=30cm2的轻质活塞放于金属筒内,封闭良好且无摩擦,一轻弹簧在筒内与活塞和筒底部同时接触,处于自然章台,已知弹簧劲度系数k=625N/m,原长L0=20cm,环境温度恒定,大气压P0=1.0×105Pa,现在活塞上方放一质量m=10kg的物块,重力加速度g=10m/s,求稳定后弹簧的压缩量. 如图所示,质量为m=2kg的物块放在一固定斜面上,斜面长L=11m,当斜面倾角为37°时物块恰能沿斜面匀速下滑.现对物体施加一大小为F=100N的水平向右恒力,可使物体从斜面底端由静止开始向上滑行,求(已知sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,质量为m=2kg的物块放在一固定斜面上,斜面长L=11m,当斜面倾角为37°时物块恰能沿斜面匀速下滑.现对物体施加一大小为F=100N的水平向右恒力,可使物体从斜面底端由静止开始向上滑行,求(已知sin37°=0.6,cos37°=0.8,g=10m/s2) 如图,在水平桌面上用硬纸板做成一个斜面,使一个钢球从斜面上某一位置滚下,钢球沿桌面飞出后做平抛运动,用一把刻度尺可以测量出钢球在水平桌面上运动的速度.具体做法是:
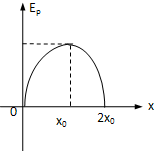
如图,在水平桌面上用硬纸板做成一个斜面,使一个钢球从斜面上某一位置滚下,钢球沿桌面飞出后做平抛运动,用一把刻度尺可以测量出钢球在水平桌面上运动的速度.具体做法是: 如图所示,一质量为m的滑块以初速度v0从固定于地面的斜面底端A开始冲上斜面,到达某一高度后返回A,斜面与滑块之间有摩擦.EK代表动能,E代表机械能,EP代表势能,a代表加速度,x代表路程,t代表时间,下图中能正确反映物理量之间关系的图象是( )
如图所示,一质量为m的滑块以初速度v0从固定于地面的斜面底端A开始冲上斜面,到达某一高度后返回A,斜面与滑块之间有摩擦.EK代表动能,E代表机械能,EP代表势能,a代表加速度,x代表路程,t代表时间,下图中能正确反映物理量之间关系的图象是( )