题目内容
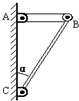（2002?天津）图中AC为竖直墙面，AB为均匀横梁，其重为G，处于水平位置．BC为支撑横梁的轻杆，它与竖直方向成α角．A、B、C三处均用铰链光滑连接．轻杆所承受的力为（ ）分析：BC为轻杆，受到两个力作用，平衡时必定共线，可判断出BC杆对横梁AB的作用力方向，以A为支点，根据力矩平衡条件求解轻杆BC对AB的作用力．
解答：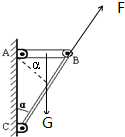
解：由题，BC为轻杆，受到两个力作用，平衡时必定共线，则知BC杆对横梁AB的作用力方向沿CB方向向上，如图．设AB长为L，以A为支点，对AB，根据力矩平衡条件得：
G
=FLcosα
解得：F=
则根据牛顿第三定律得知，轻杆所承受的力为：F′=F=
故选D
解：由题，BC为轻杆，受到两个力作用，平衡时必定共线，则知BC杆对横梁AB的作用力方向沿CB方向向上，如图．设AB长为L，以A为支点，对AB，根据力矩平衡条件得：G
| L |
| 2 |
解得：F=
| G |
| 2cosα |
则根据牛顿第三定律得知，轻杆所承受的力为：F′=F=
| G |
| 2cosα |
故选D
点评：本题是力平衡问题和力矩平衡问题的综合，关键是根据BC是二力杆，确定出BC对AB的作用力方向．
练习册系列答案
相关题目
（2002?天津）有三根长度皆为l=1.00m的不可伸长的绝缘轻线，其中两根的一端固定在天花板上的 O点，另一端分别挂有质量皆为m=1.00×10-2 kg的带电小球A和B，它们的电量分别为一q和+q，q=1.00×10-7C．A、B之间用第三根线连接起来．空间中存在大小为E=1.00×106N/C的匀强电场，场强方向沿水平向右，平衡时 A、B球的位置如图所示．现将O、B之间的线烧断，由于有空气阻力，A、B球最后会达到新的平衡位置．求最后两球的机械能与电势能的总和与烧断前相比改变了多少．（不计两带电小球间相互作用的静电力）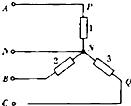
（2002?天津）在三相交流电源上按星形接法连接相同负载1、2、3，如图所示，NN′是中性线．已知负载1上的电压为220V，电流强度为15A．现以I表示中性线上的电流，U表示图中P、Q两点之间的电压，则
（2002?天津）图中MN、GH为平行导轨，AB、CD为跨在导轨上的两根横杆，导轨和横杆均为导体．有匀强磁场垂直于导轨所在的平面，方向如图．用I表示回路中的电流．（ ）