题目内容
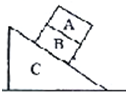 固定在地面上的粗糙斜面C倾角为θ,上有两个矩形物块A、B,质量分别为ml和m2,A、B两物块之间的动摩擦因数为μ1,B与斜面C之间的动摩擦因数为μ2,现将A、B从斜面顶端由静止开始释放( )
固定在地面上的粗糙斜面C倾角为θ,上有两个矩形物块A、B,质量分别为ml和m2,A、B两物块之间的动摩擦因数为μ1,B与斜面C之间的动摩擦因数为μ2,现将A、B从斜面顶端由静止开始释放( )分析:假设两物体相对静止,先对整体根据牛顿第二定律求出加速度,再隔离A研究,求出A受到的静摩擦力,与A的最大静摩擦力比较,分析两者加速度能否相同.
解答:解:
A、B假设A、B相对静止,加速度相同,根据牛顿第二定律得
对整体:加速度为a=
=g(sinθ-μ2cosθ)
对A:设A所受的摩擦力方向沿斜面向上,则有
m1gsinθ-f=m1a,得f=μ2m1gcosθ
A所受的最大静摩擦力为fm=μ1m1gcosθ
若μ1>μ2,则f<fm,则说明两物体相对静止,加速度相同.故A错误,B正确.
C、D若μ1<μ2,则f>fm,不可能,说明两物体相对运动,加速度不同.故CD错误.
故选B
A、B假设A、B相对静止,加速度相同,根据牛顿第二定律得
对整体:加速度为a=
| (mA+mB)gsinθ-μ(mA+mB)gcosθ |
| mA+mB |
对A:设A所受的摩擦力方向沿斜面向上,则有
m1gsinθ-f=m1a,得f=μ2m1gcosθ
A所受的最大静摩擦力为fm=μ1m1gcosθ
若μ1>μ2,则f<fm,则说明两物体相对静止,加速度相同.故A错误,B正确.
C、D若μ1<μ2,则f>fm,不可能,说明两物体相对运动,加速度不同.故CD错误.
故选B
点评:本题是两个物体的连接体问题,采用假设法研究,要抓住它们加速度相同的特点,灵活运用整体法和隔离法研究.

练习册系列答案
相关题目
 如图所示,固定在地面上的粗糙绝缘斜面ABCD的倾角为θ,空间中存在着与AB边平行的水平匀强电场,场强大小为E.将一个带正电的小物块(可视为质点)放置在这个斜面上,小物块质量为m,所带电荷量为q,与斜面间的动摩擦因数u.若小物块静止,则下列说法中正确的是( )
如图所示,固定在地面上的粗糙绝缘斜面ABCD的倾角为θ,空间中存在着与AB边平行的水平匀强电场,场强大小为E.将一个带正电的小物块(可视为质点)放置在这个斜面上,小物块质量为m,所带电荷量为q,与斜面间的动摩擦因数u.若小物块静止,则下列说法中正确的是( )


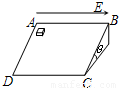 如图所示,固定在地面上的粗糙绝缘斜面ABCD的倾角为θ,空间中存在着与AB边平行的水平匀强电场,场强大小为E.将一个带正电的小物块(可视为质点)放置在这个斜面上,小物块质量为m,所带电荷量为q,与斜面间的动摩擦因数u.若小物块静止,则下列说法中正确的是( )
如图所示,固定在地面上的粗糙绝缘斜面ABCD的倾角为θ,空间中存在着与AB边平行的水平匀强电场,场强大小为E.将一个带正电的小物块(可视为质点)放置在这个斜面上,小物块质量为m,所带电荷量为q,与斜面间的动摩擦因数u.若小物块静止,则下列说法中正确的是( ) 如图所示,固定在地面上的粗糙绝缘斜面ABCD的倾角为θ,空间中存在着与AB边平行的水平匀强电场,场强大小为E.将一个带正电的小物块(可视为质点)放置在这个斜面上,小物块质量为m,所带电荷量为q,与斜面间的动摩擦因数u.若小物块静止,则下列说法中正确的是( )
如图所示,固定在地面上的粗糙绝缘斜面ABCD的倾角为θ,空间中存在着与AB边平行的水平匀强电场,场强大小为E.将一个带正电的小物块(可视为质点)放置在这个斜面上,小物块质量为m,所带电荷量为q,与斜面间的动摩擦因数u.若小物块静止,则下列说法中正确的是( )