题目内容
【题目】某校举行托乒乓球跑步比赛,赛道为水平直道,比赛距离为S。比赛时,某同学将球置于球拍中心,以大小为a的加速度从静止开始做匀加速直线运动,当速度达到![]() 时,再以
时,再以![]() 做匀速直线运动跑至终点。整个过程中球一直保持在球拍中心不动。比赛中,该同学在匀速直线运动阶段保持球拍的倾角为
做匀速直线运动跑至终点。整个过程中球一直保持在球拍中心不动。比赛中,该同学在匀速直线运动阶段保持球拍的倾角为![]() ,如图所示。设球在运动中受到空气阻力大小与其速度大小成正比(
,如图所示。设球在运动中受到空气阻力大小与其速度大小成正比(![]() ),方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g。
),方向与运动方向相反,不计球与球拍之间的摩擦,球的质量为m,重力加速度为g。
(1)求空气阻力大小与球速大小的比例系数![]() ;
;
(2)求在加速跑阶段球拍倾角![]() 随速度
随速度![]() 变化的关系式;
变化的关系式;
(3)整个匀速跑阶段,若该同学速度仍为![]() ,而球拍的倾角比
,而球拍的倾角比![]() 大了
大了![]() 并保持不变,不计球在球拍上的移动引起的空气阻力变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求
并保持不变,不计球在球拍上的移动引起的空气阻力变化,为保证到达终点前球不从球拍上距离中心为r的下边沿掉落,求![]() 应满足的条件。
应满足的条件。

【答案】(1)![]() ,(2)
,(2)![]() ,(3)
,(3)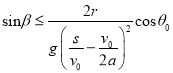 .
.
【解析】试题分析:(1)在匀速运动阶段,受力平衡,根据平衡条件列式即可求解;(2)加速阶段,设球拍对球的支持力为![]() ,根据牛顿第二定律即可求解;(3)根据牛顿第二定律求出球沿球拍面下滑的加速度,当球运动的位移小于等于r时,球不从球拍上掉落,根据运动学基本公式列式即可求解.
,根据牛顿第二定律即可求解;(3)根据牛顿第二定律求出球沿球拍面下滑的加速度,当球运动的位移小于等于r时,球不从球拍上掉落,根据运动学基本公式列式即可求解.
(1)在匀速运动阶段,有: ![]()
得: ![]()
(2)加速阶段,设球拍对球的支持力为![]() ,有:
,有:
由牛顿第二定律得: ![]()
由平衡条件得: ![]()
联立得: ![]()
(3)以速度![]() 匀速运动时,设空气阻力与重力的合力为F,则有
匀速运动时,设空气阻力与重力的合力为F,则有![]()
球拍倾角为![]() 时,空气阻力与重力的合力不变,设球沿球拍面下滑的加速度大小为
时,空气阻力与重力的合力不变,设球沿球拍面下滑的加速度大小为![]()
由牛顿第二定律得: ![]()
设匀速跑阶段所用时间为t,有: ![]()
球不从球拍上掉落的条件![]()
联立得: 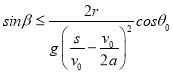

练习册系列答案
相关题目










